Active and passive hybrid vibration control and analysis of dike pipeline
-
摘要:
针对泵站机组运行引起的供排水穿堤管道振动问题，该研究提出一种磁流变阻尼器(magnetorheological damper，MRD)-谐调质量阻尼器(tune mass damper，TMD)有机融合(magnetorheological-tune mass damper，MRTMD)的主被动混合控制体系。利用基于线性二次型(linear quadratic regulator，LQR)最优控制算法，以结构响应加速度取最小为目标函数，优化得到主被动混合振动控制体系相关参数，以提高减振效率和稳定性。通过模拟泵站运行荷载与冲击荷载激励下的结构动力响应控制效果分析，探讨混合控制装置输出阻尼力的鲁棒性和减振效果。将MRTMD应用于穿堤管道工程，从时频域角度分析了所提出的主被动混合控制体系减振效率与有效减振频带范围，结果表明：MRTMD对结构振动耗能能力强，减振频带范围广，效果优于单一的TMD和MRD控制；针对穿堤管道结构振动响应的控制效果良好，加速度响应减振效率达到37.56%～38.07%，位移响应减振效率达到40.23%～41.38%；对机组主轴转动引起的转频、倍频等机械振动均可有效减弱，特别是对水流冲击、叶轮内形成的轴向漩涡造成的中低振动频率减振效果显著。该方法可为穿堤管道结构减振控制提供参考，保障穿堤管道结构安全运行。
Abstract:An active passive hybrid control system (MRTMD) was proposed to combine a magnetorheological damper (MRD) and a tuned mass damper (TMD). The vibration of water supply and drainage pipelines was controlled when passing through embankments caused by the operation of pumping station units. Linear quadratic regulator (LQR) based optimal control algorithm was utilized to optimize the parameters of the active passive hybrid vibration control system, in order to minimize the acceleration of the structure. Magnetorheological damper damping was stable enough to change the damping frequency in the new system, compared with the traditional single-tuned mass damper. Firstly, a simulation signal was constructed to simulate the load excitation of pump station units during operation, the vibration response of pump station pipeline was also used to compare with a single TMD and MRD control, in order to verify the applicability and effectiveness of the MRTMD for pump station pipeline vibration reduction. Secondly, shock waves were used as excitation to simulate and analyze the control effect of pipeline dynamic response, in response to the phenomenon of water hammer during opening and closing of the unit or the abnormal vibration under extreme working conditions. The damping force and displacement hysteresis curve were used to explore the robustness and vibration reduction of the output resistance force; Finally, MRTMD was applied to the water supply and drainage pipeline project in the Beijiang Dam in Guangdong Province. The simplified two-degree-of-freedom mass, stiffness, and damping matrices of the pipeline were solved using load inversion and then established the pipeline vibration dynamics equation. Taking the vibration reduction efficiency as the evaluation index, the vibration reduction efficiency of the new system on the water supply and drainage pipeline structure passing through the embankment was analyzed from the time domain perspective. The effective vibration reduction frequency range and energy reduction efficiency of each main frequency of MRTMD were also analyzed from the frequency domain perspective. The results show that the damping force provided by MRTMD shared a wide range, stable output, and strong energy dissipation. Better control was achieved in the acceleration response of pipeline structure, when passing through the embankment, with a damping efficiency of 37.56%-38.07%. There was a slightly better control in the displacement response of the structure, compared with the acceleration response, with a damping efficiency of 40.23%-41.38%, and a damping effect of 33.9% at the pipeline passing through the embankment. The vibration reduction was superior to single TMD and MRD control; There was the weakening effect of MRTMD on the main frequency energy of various vibration sources during operation in a frequency domain. Among them, the mechanical vibration energy caused by the rotation of the main shaft (such as rotation frequency and doubling frequency) was reduced to 27.46% and 75.88%, respectively, while the vibration energy was significantly reduced to 36.46% for medium to low frequency vibration that caused by water flow impact and axial vortices formed in the impeller.
-
Keywords:
- vibration /
- acceleration /
- pipeline /
- active passive hybrid control /
- magnetorheological damper /
- tuned mass damper
-
0. 引 言
随着基础建设的日益完善，管道工程在农业灌溉领域中的地位越来越重要，扮演了为农业生产供水，疏导汛期积水等重要作用[1-4]。工程实践表明，供排水穿堤管道在机组运行时会产生持续振动，采用隔振支座、设置镇墩等方式已经难以实现对管道结构长时间、高内力的有效减振。因此，确保在长时间、高频率振源激励作用下穿堤管道工程安全稳定运行已经成为急需解决的关键问题。大量研究表明，在结构上布置减振装置，可以减弱结构动力响应，提高结构在振动中的稳定性[5]，而主被动混合控制技术兼具主动控制出色的自适应控制与被动控制可靠的稳定性，对主被动混合控制技术的研究已成为国内外振动控制领域的热点课题[6-7]。
目前，国内外学者针对被动控制、主动控制以及混合控制进行了一系列研究。被动控制具有结构简单、稳定性强等特点，但是对于特定频率外界激励则不能很好的减小振动响应，对激励环境变化的适应性较差[8-10]。在实际工程中，多种荷载共同激励，使得结构产生高阶振动模态，采用常规的被动谐调质量阻尼器(tune mass damper，TMD)对结构进行减振，减振效果会大大降低甚至造成抑振失效[11]。主动控制可以弥补被动控制的不足，具有很强的环境适应能力，调控频率宽且响应较快，但需要外接电源来控制阻尼器输出，遭遇到极端天气或外部能量输入不稳定时，阻尼器很难实时输出阻尼力，存在潜在的不稳定性[12-13]。刘彦辉等[14]提出了针对地震和风振激励下的主被动复合调谐控制策略，对控制效果与减振机理分析，完成了主被动复合调谐控制振动台试验，为工程应用提供了支撑。廖英英等[15]采用两种半主动混合控制，对随机激励下的模型仿真分析表明，该新型混合控制策略扩大了减振频率范围。周亚丽等[16]基于仿真试验，采用主动-被动混合控制方法，开展了压电智能结构振动控制研究，得出了该方法能够降低结构振动响应。马小陆等[17]提出了一种主-被动混合控制策略，结合压电材料的特性与小波自适应主动控制的优点，主、被动控制相互弥补，通过仿真和物理模型实验证明该方法能够有效抑制结构振动，减振效率达到80%以上。赵祥昇等[18]提出了液体黏滞阻尼器与调谐质量阻尼器并联的混合控制方法，研究不同阻尼指数对减振系统的影响，结果表明其鲁棒性显著提高，同时对阻尼系数的需求显著降低。张延年等[19]采用磁流变阻尼器与铅芯橡胶垫，提出了3种混合控制方案，并进行地震反应分析，对加速度减振效率最大达到25.18%，控制效果明显。王海军等[20]建立有限元模型，确定水力脉动荷载计算方法，研究管道水力振动的传播规律，为减振提供技术支撑。KHAZAEE等[21]提出了一种被动非线性吸振器，通过线性弹簧、轻质量块和线性阻尼器组成并与管道连接，实现对管道的振动控制。BORGI等[22]建立有限元模型，沿管道布置调谐局部谐振器，研究了管道系统在共振频率下的振动衰减。张翌娜等[23]以输水管道为例，分析TMD系统的减振效果，结果表明，多个TMD减振系统可达到更优的管道减振效果。综上分析，目前管道减振研究多集中在被动控制，主被动控制融合的方法应用于管道的报道较少，为克服以往管道被动控制无法改变减振频率的问题，弥补主动控制需要外界能量和出力不稳定的不足，提高管道结构减振效率和可靠性，保障运行安全，开展管道结构减振控制系统研究十分必要。
本文提出一种磁流变阻尼器(magnetorheological damper，MRD)和调谐质量阻尼器(tune mass damper，TMD)有机融合(MRTMD)的主被动混合控制体系。针对广州北江大堤供排水穿堤管道进行振动控制研究，对比单一TMD、MRD控制，以减振效率为指标，对MRTMD减振效率进行评估，分析阻尼力输出的稳定性，得出有效减振频域区间，拟为工程应用提供支撑。
1. 混合控制系统及模型
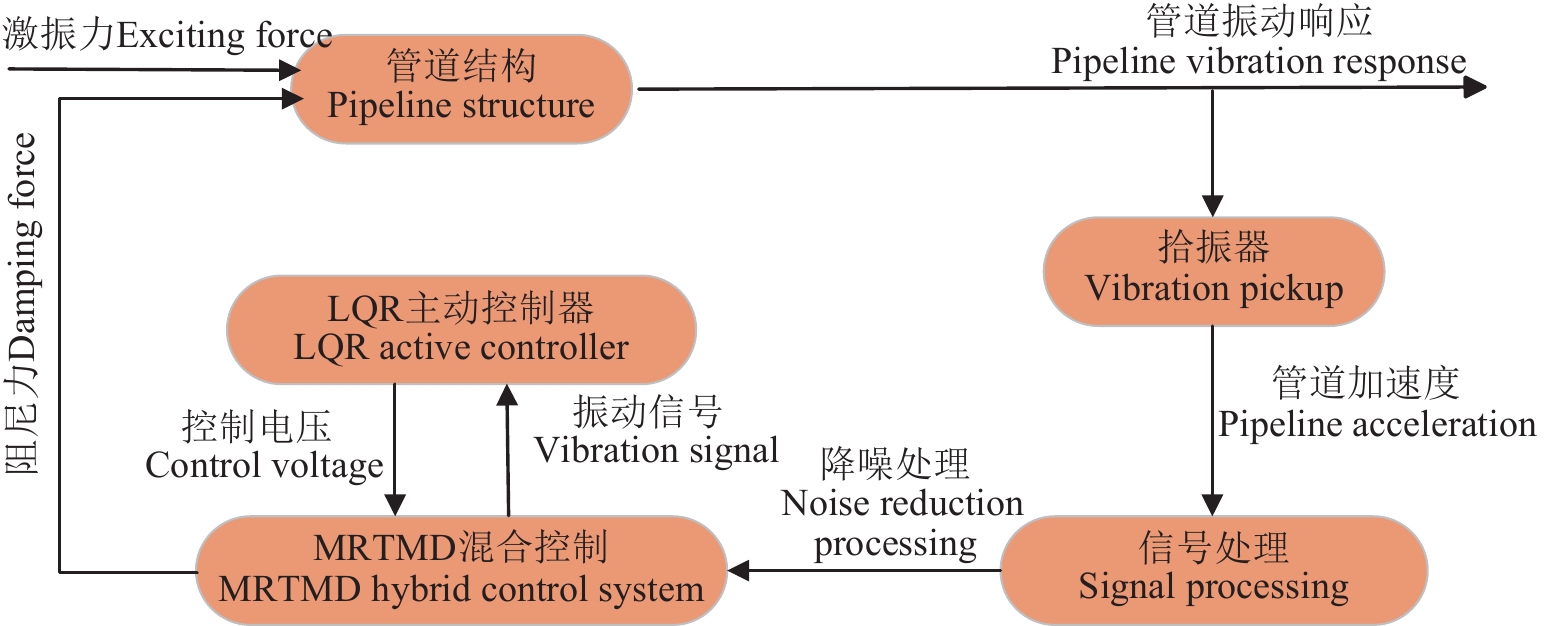
MRTMD主被动混合控制系统是在基于线性二次型(linear quadratic regulator，LQR)主动控制的磁流变阻尼器的基础上，将控制模块与能量输出模块结合，通过附加一定的质量形成满足相应频率的TMD质量块，从而使得TMD与磁流变阻尼器协调工作，达到更优的减振效果，提出的主被动混合控制系统动力学模型如图1所示。
构建多自由度结构的MRTMD减振系统，其运动方程如式(1)所示。
$$ \left\{ \begin{gathered} {\boldsymbol{M\ddot X}} + {\boldsymbol{C\dot X}} + {\boldsymbol{KX}} = - {\boldsymbol{M}}{{\boldsymbol{D}}_s}{{\ddot x}_g} + {{\boldsymbol{B}}_s}{f_c}\left( t \right) \\ {\boldsymbol{X}}\left( {{t_0}} \right) = {{\boldsymbol{X}}_0} \\ {\boldsymbol{\dot X}}\left( {{t_0}} \right) = {{{\boldsymbol{\dot X}}}_0} \\ \end{gathered} \right. $$ (1) 式中$ {\ddot x_g}$为外界激励下的结构振动加速度响应；$ {{\boldsymbol{D}}_s} $为外界激励的位置矩阵；$ {{\boldsymbol{B}}_s} $为多自由度系统控制力位置矩阵；$ {f_c}\left( t \right) $为控制系统的控制力；$ {\boldsymbol{X}}\left( {{t_0}} \right) $和$ {\boldsymbol{\dot X}}\left( {{t_0}} \right) $分别是结构初始位移向量和初始速度向量；$ {\boldsymbol{X}} $,$ {\boldsymbol{\dot X}} $和$ {\boldsymbol{\ddot X}} $分别为MRTMD控制系统的位移响应、速度响应和加速度响应，$ {\boldsymbol{X}} = {\left\{ {{x_1},{x_2}, \cdots ,{x_n},{x_t},{x_d},} \right\}^{\rm T}} $；$ {\boldsymbol{M}} $，$ {\boldsymbol{C}} $和$ {\boldsymbol{K}} $分别为MRTMD控制系统质量矩阵、阻尼矩阵和刚度矩阵。
$ {\boldsymbol{M}} $、$ {\boldsymbol{C}} $、$ {\boldsymbol{K}} $分别为
$$ {\boldsymbol{M}} = \left[ {\begin{array}{*{20}{l}} {{m_1}}&{}&{}&{}&{} \\ {}& \ddots &{}&{}&{} \\ {}&{}&{{m_n}}&{}&{} \\ {}&{}&{}&{{m_t}}&{} \\ {}&{}&{}&{}&{{m_d}} \end{array}} \right] $$ $$ {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{c_{11}}}& \cdots &{{c_{1n}}}&0&0 \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ {{c_{n1}}}& \cdots &{{c_{nn}} + {c_t}}&{ - {c_t}}&0 \\ 0& \cdots &{ - {c_t}}&{{c_t} + {c_d}}&{ - {c_d}} \\ 0& \cdots &0&{ - {c_d}}&{{c_d}} \end{array}} \right] $$ $$ {\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {{k_{11}}}& \cdots &{{k_{1n}}}&0&0 \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ {{k_{n1}}}& \cdots &{{k_{nn}} + {k_t}}&{ - {k_t}}&0 \\ 0& \cdots &{ - {k_t}}&{{k_t} + {k_d}}&{ - {k_d}} \\ 0& \cdots &0&{ - {k_d}}&{{k_d}} \end{array}} \right] $$ 式中，mi，mt和md分别为结构、TMD和MRD的质量，kg；cij，ct和cd分别为结构、TMD和MRD的阻尼系数；kij，kt和kd分别为结构、TMD和MRD的刚度系数。
TMD系统减振带宽较窄，且仅在一定的固有频率或较窄的频率范围内可以取得良好的减振效率，当被控结构的振动频率范围较广时，其减振效率明显降低。因此，不同工况下MRTMD系统中的关键是调整TMD系统的固有频率，使其与被控结构的固有频率接近。根据式(2)确定被控结构与TMD的固有频率$ {\mathbf{\omega }} $（rad/s）[24]。
$$ {\boldsymbol{\omega }} = \sqrt {{{\boldsymbol{K}} \mathord{\left/ {\vphantom {{\boldsymbol{K}} {\boldsymbol{M}}}} \right. } {\boldsymbol{M}}}} $$ (2) 依据被控结构所设计出MRTMD系统，将整个体系运动方程用状态空间方程表达为
$$ {\boldsymbol{\dot Z = AZ}} + {\boldsymbol{B}}{f_c}\left( t \right) + {\boldsymbol{E}}{\ddot x_g}\left( t \right) $$ (3) $$ {\boldsymbol{y = CZ + D}}{f_c}\left( t \right) + {\boldsymbol{W}}{\ddot x_g}\left( t \right) $$ (4) 式中$ {\boldsymbol{Z = }}\left[ \begin{gathered} {\boldsymbol{X}} \\ {{\boldsymbol{\dot X}}} \\ \end{gathered} \right] $为系统的状态向量；$ {\boldsymbol{y}} $为输出矩阵；$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&{\boldsymbol{I}} \\ { - {{\boldsymbol{M}}^{ - 1}}{\boldsymbol{K}}}&{ - {{\boldsymbol{M}}^{ - 1}}{\boldsymbol{C}}} \end{array}} \right] $；$ {\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}} 0 \\ {{{\boldsymbol{M}}^{ - 1}}{{\boldsymbol{B}}_s}} \end{array}} \right] $；$ {\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ { - 1} \end{array}} \right] $；$ {\boldsymbol{C = }}\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \\ { - {{\boldsymbol{M}}^{ - 1}}{\boldsymbol{K}}}&{ - {{\boldsymbol{M}}^{ - 1}}{\boldsymbol{C}}} \end{array}} \right] $；$ {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ {{{\boldsymbol{M}}^{ - 1}}{{\boldsymbol{B}}_s}} \end{array}} \right] $。
采用LQR最优控制作为MRD的主动控制算法，LQR控制算法的核心问题是选择合理权矩阵Q、R使得目标函数取最小值。以管道结构振动响应加速度为LQR目标函数，从而计算得到相关参数，LQR目标性能函数[7]为
$$ {\boldsymbol{J}} = \frac{1}{2}\int_{{t_0}}^\infty {\left[ {{{\boldsymbol{Z}}^{\rm T}}\left( t \right){\boldsymbol{QZ}}\left( t \right) + {{\boldsymbol{U}}^{\rm T}}\left( t \right){\boldsymbol{RU}}\left( t \right)} \right]} {\text{d}}t $$ (5) 式中Q为算法结构反应权矩阵，通过增加Q减小被控结构的反应，达到增强控制效果的目的；R为算法控制力权矩阵，减小R可以提高减振性能，但也会增加控制力U(t)的输入，消耗更多能量。
2. 振动控制仿真分析
通过建立单自由度体系，对比不同荷载激励作用下MRTMD与TMD和MRD的减振效果，说明MRTMD减振系统的有效性。首先，设定模型结构的质量为1600 kg，刚度为320 kN/m，阻尼系数为1250 (N·s)/m，由式(2)确定结构的固有频率为0.447 rad/s。其次，设定MRD的刚度系数和阻尼系数均为0.01；设定MRTMD模型中TMD的质量为160 kg，刚度为32 kN/m，使之与模型结构的固有频率一致。最终，分别对无减振控制结构、单一TMD减振、单一MRD减振、MRTMD减振进行结构响应分析，评价减振效率。
2.1 泵机组模拟荷载控制反馈分析
为验证MRTMD方法的有效性和对泵站管道减振的适用性，根据泵站管道振源组成，构造泵站机组运行时的荷载激励，仿真信号的计算为
$$ \left\{\begin{gathered}x_1=3\sin\left(2f_1\text{π }t\right) \\ x_2=4\sin\left(2f_2\text{π }t\right) \\ x_3=5\sin\left(2f_3\text{π }t\right) \\ x_4=4\sin\left(2f_4\text{π }t\right) \\ x_5=2\times\text{rand}\mathrm{n}\left(1\;000,1\right) \\ {\boldsymbol{X}}=x_1+x_2+x_3+x_4+x_5 \\ \end{gathered}\right. $$ (6) 式中X为谐波荷载；f1、f2、f3和f4分别为模拟机组运行工况下的各优势频率，取低频f1=6 Hz、转频f2=10 Hz、三倍频f3=30 Hz和叶频f4=60 Hz；t为时间，取10 s；randn为均值为0、方差为1、呈正态分布的随机函数。
采用均方根方法对结构响应数据进行计算，验证减振效率，评价减振效果，计算式为
$$ {X_{rms}} = \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^n {s_i^2} }}{n}} = \sqrt {\frac{{s_1^2 + s_2^2 + \cdots + s_n^2}}{n}} $$ (7) $$ Y = \frac{{{X_{rms1}} - {X_{rms2}}}}{{{X_{rms1}}}} \times 100\text{%} $$ (8) 式中$ {s_i} $为结构响应数据，n为数据总数，Xrms1为减振前结构响应数据的均方根，Xrms2为减振后结构响应数据的均方根， Y为减振效率，%。
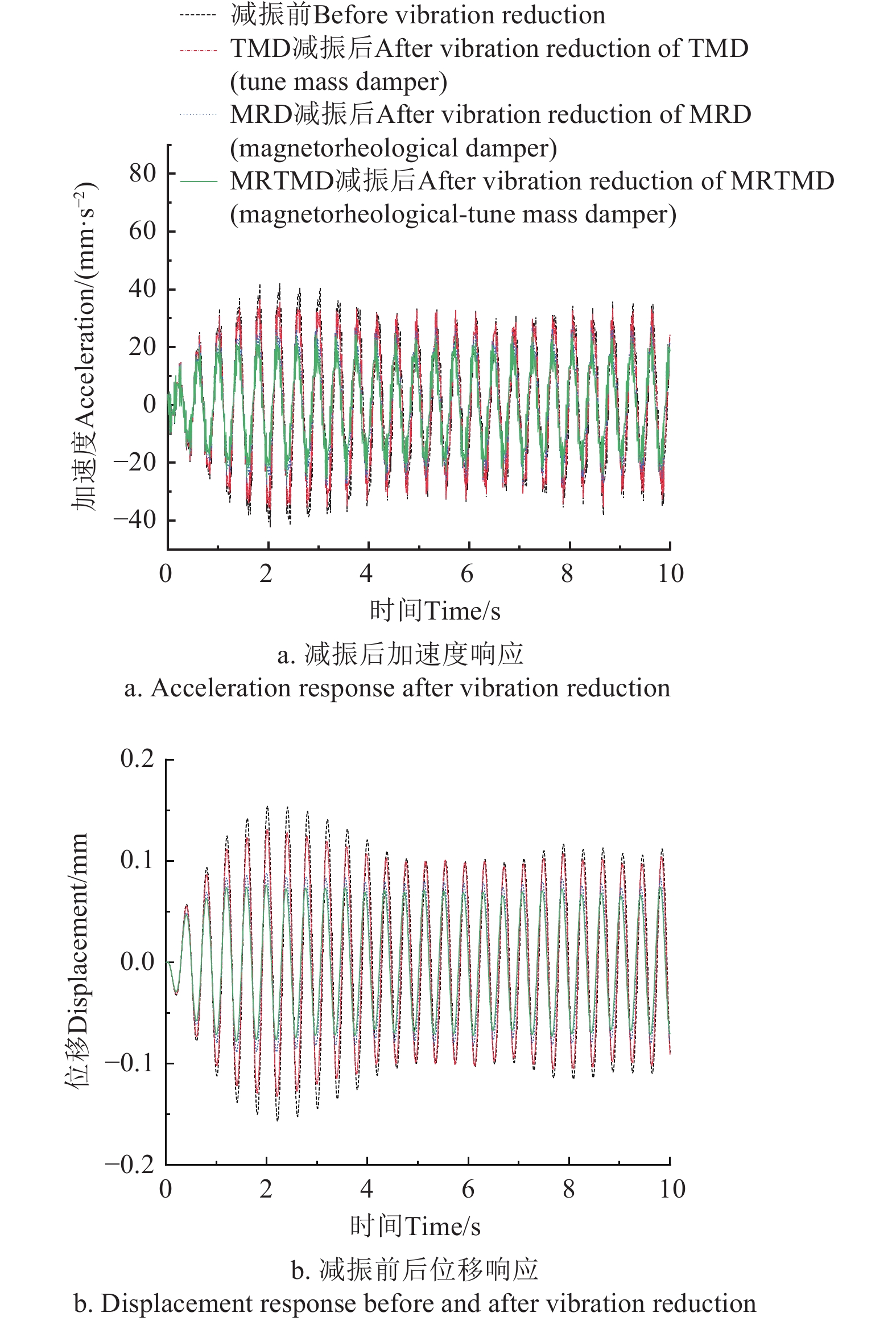
在TMD、MRD和MRTMD控制下，所构造仿真信号的加速度和位移响应如图2所示，由均方根计算减振效率见表1。由图2、表1可知，结构最大加速度与位移响应出现在2 s左右，MRTMD使得结构加速度和位移响应减小37.26%和39.85%，峰值分别降低至无减振控制状态下的40.20%和53.17%，控制效果优于单一的TMD、MRD减振；同时，图2中4～6 s左右，TMD控制效果微弱，甚至出现了放大结构响应的情况，因此，采用TMD被动控制并不能保证减振效果；基于LQR控制的单一MRD减振效果略逊于MRTMD混合控制，且MRTMD混合控制的响应均方根值更小，说明在实际中选用MRTMD，不仅能获得更出色的减振效果，还能保证具有更高的容错率。
表 1 谐波激励下结构响应均方根值及减振效率Table 1. Root mean square value and vibration reduction efficiency of structural response under harmonic excitation减振措施
Vibration
reduction
measures响应均方根值
Root mean square of response减振效率
Vibration reduction efficiency加速度Accelaration/
(mm·s−2)位移Displacement/
mm加速度Accelaration/
%位移Displacement/
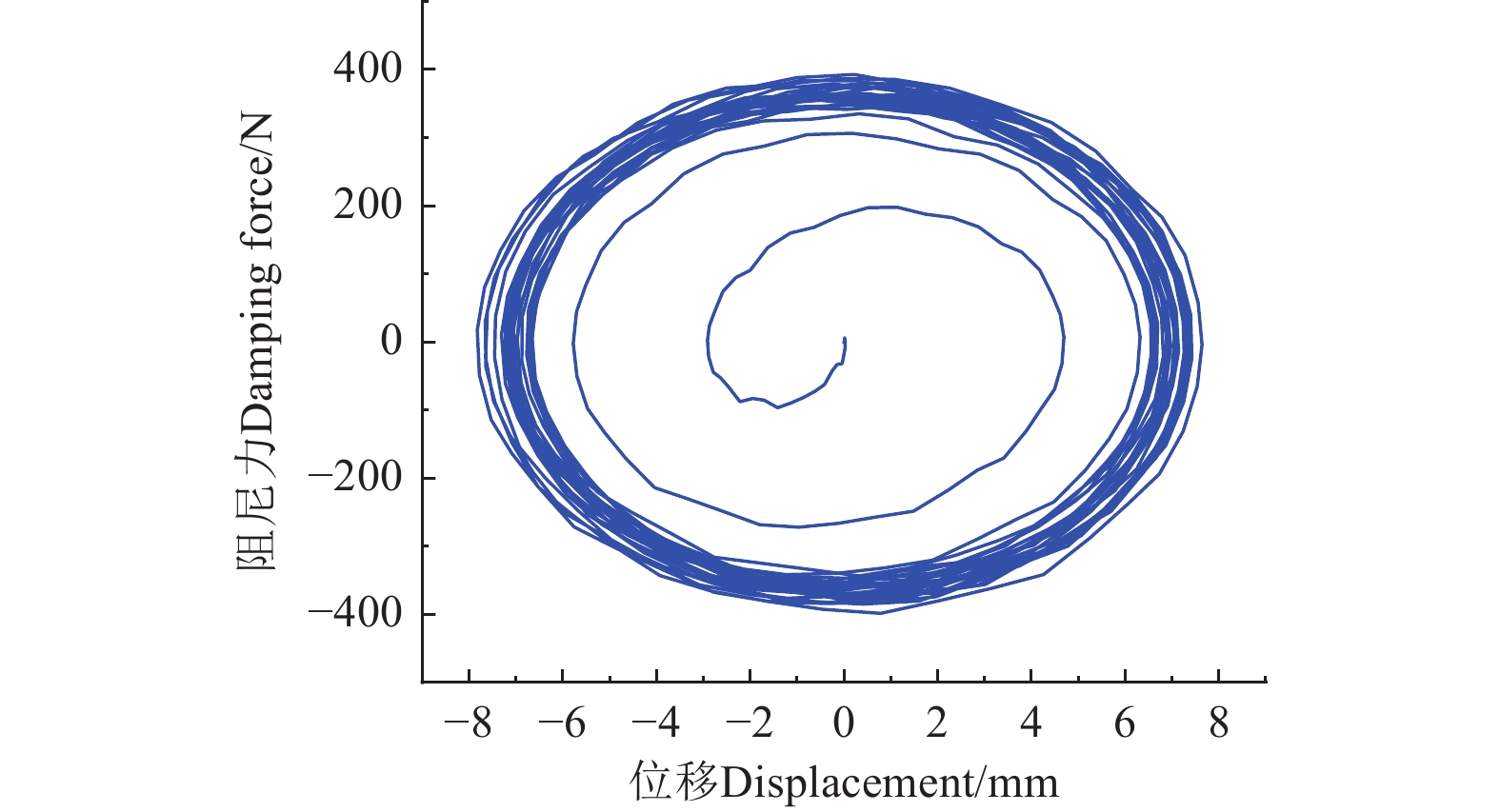
%无控(减振前) 21.14 0.08 / / TMD 19.30 0.07 8.71 9.50 MRD 14.79 0.06 30.07 32.19 MRTMD 13.26 0.05 37.26 39.85 ![]()
图 2 不同控制方法下结构加速度和位移响应对比(谐波)Figure 2. Comparison of structural acceleration and displacement response under different control methods (harmonic)阻尼力与位移滞回曲线是反应阻尼器出力稳定性的重要方式，谐波激励下MRTMD的阻尼力与位移滞回曲线如图3所示，当滞回曲线中位移幅值大于7 mm时，MRTMD的阻尼力可达到390 N，滞回环近似圆形，曲线饱满，无间断、突变点，阻尼力幅值随位移的增大而增大，说明MRTMD能够自适应跟踪结构响应、实现对结构最优控制力的输出，提供的阻尼力稳定，对结构的振动能量耗散效果好，耗能能力强。
2.2 极端荷载控制反馈分析
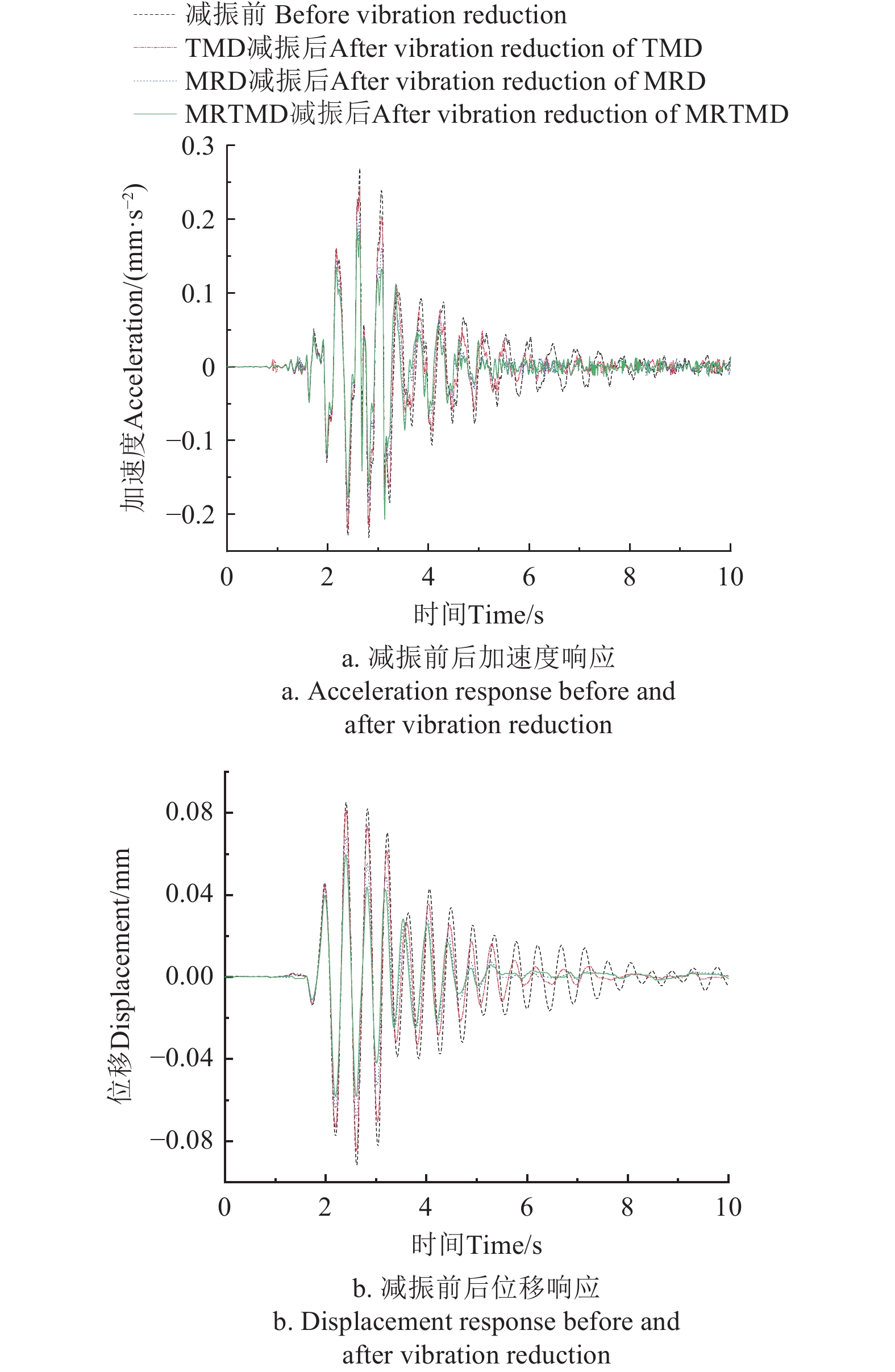
采用冲击荷载作为极端作用，模拟机组启闭过程中由于水锤等原因造成的冲击振动响应。对比TMD、MRD和MRTMD控制，结构的加速度和位移响应如图4所示，由均方根计算减振效率见表2。由图4、表2可知，冲击荷载对结构产生的振动主要集中在2 s到6 s，MRTMD对冲击荷载作用下结构的加速度和位移响应减小30.51%和39.46%，峰值分别降低至无减振控制状态下的70%和71%，且MRTMD混合控制响应均方根值依旧最小，控制效果优于单一的TMD、MRD减振。
![]()
图 4 不同控制方法下结构加速度和位移响应对比(冲击荷载)Figure 4. Comparison of structural acceleration and displacement response under different control methods (shock excitation)从图4可以看出，TMD针对冲击荷载作用下结构振动的峰值减振效果并不理想，在TMD的基础上联合基于LQR主动控制的磁流变阻尼器，可有效降低冲击荷载作用在结构上的响应峰值。因此，在结构上设置MRTMD混合控制装置，极端工况下对结构的振动响应控制仍有良好的效果。
表 2 冲击荷载激励下结构响应均方根值及减振效率Table 2. Root mean square value and vibration reduction efficiency of structural response under shock wave excitation减振措施
Vibration
reduction
measures响应均方根值
Root mean square of response减振效率
Vibration reduction efficiency加速度Accelaration/
(mm·s−2)位移Displacement/
mm加速度Accelaration/
%位移Displacement/
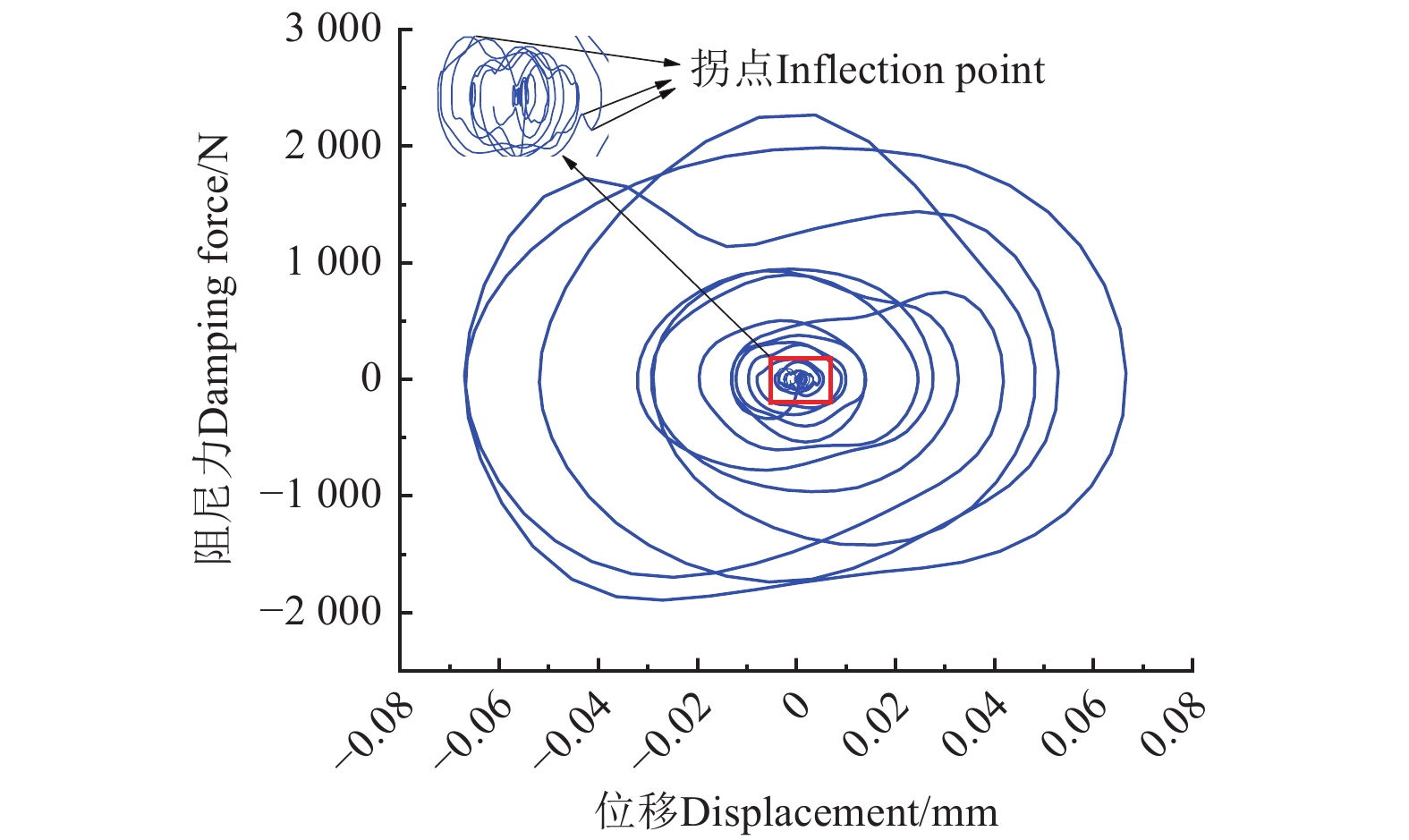
%无控(减振前) 5.76 2.4×10−2 − − TMD 5.22 2.1×10−2 9.34 13.19 MRD 4.42 1.7×10−2 23.30 30.37 MRTMD 4.00 1.4×10−2 30.51 39.46 冲击波激励下的MRTMD的阻尼力与位移滞回曲线如图5所示，在极端工况下，滞回环呈椭圆形，曲线总体饱满，无间断、突变点，阻尼力幅值随位移的增大而增大，说明MRTMD能够自适应跟踪结构响应、实现对结构最优控制力的输出，提供的阻尼力稳定，对结构振动能量耗能能力较好。图5曲线中为数不多的拐点为荷载突然变大时MRTMD提供阻尼力短暂的滞后现象，对应图4中，加速度与速度时程曲线2 s前后荷载突然变大。经过短暂的迟滞，MRTMD可迅速输出阻尼力，减弱结构振动响应。
3. 工程实例
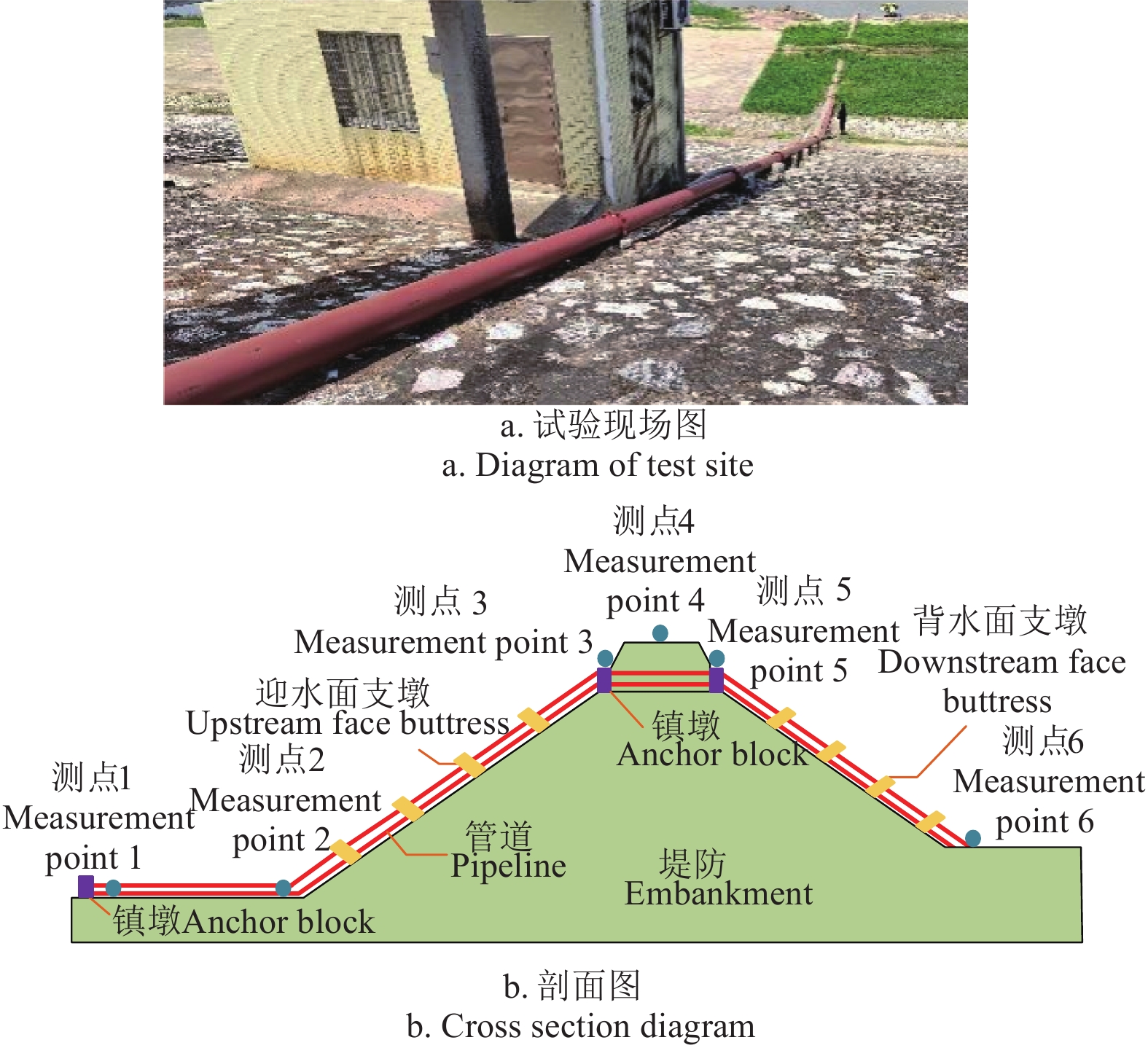
北江大堤位于广东省北江下游左岸，关系到广州市的防洪安全，兼顾农田灌溉、城市供水等作用。为了减小管道振动对穿堤处土体的影响，保证堤防结构安全稳定，将MRTMD混合控制应用于穿堤管道结构，具体分为以下几步完成：首先，管道振动信息采集采用941B型振动传感器，灵敏度为0.3 V·s/m，能够实现超低频（低至0.17 Hz）振动测量。其次，测点布置按照北江大堤穿堤管道现场图与剖面图确定，如图6所示，图6b中测点1为泵站管道引水处，此处所测量的振动响应最大；测点2为管道爬坡处，此处管道发生弯折，水流流态复杂；测点3处为管道穿堤入口端，该处振动响应的大小直接影响堤防穿堤部位的结构安全。最后，由于在测点3和迎水坡坡面不便安装MRTMD混合控制装置，故选择在测点1、测点2处分别设置MRTMD，验证控制效果。
![]()
图 6 北江大堤穿堤管道现场图与剖面图Figure 6. On site and cross-sectional view of the pipeline crossing the Beijiang embankment3.1 荷载反演
为准确获得MRTMD减振后北江大堤穿堤管道振动响应数据，有效验证MRTMD应用于工程的减振效果，需根据现场实测管道响应数据和穿堤管道有限元模型开展荷载反演获得管道激振力。
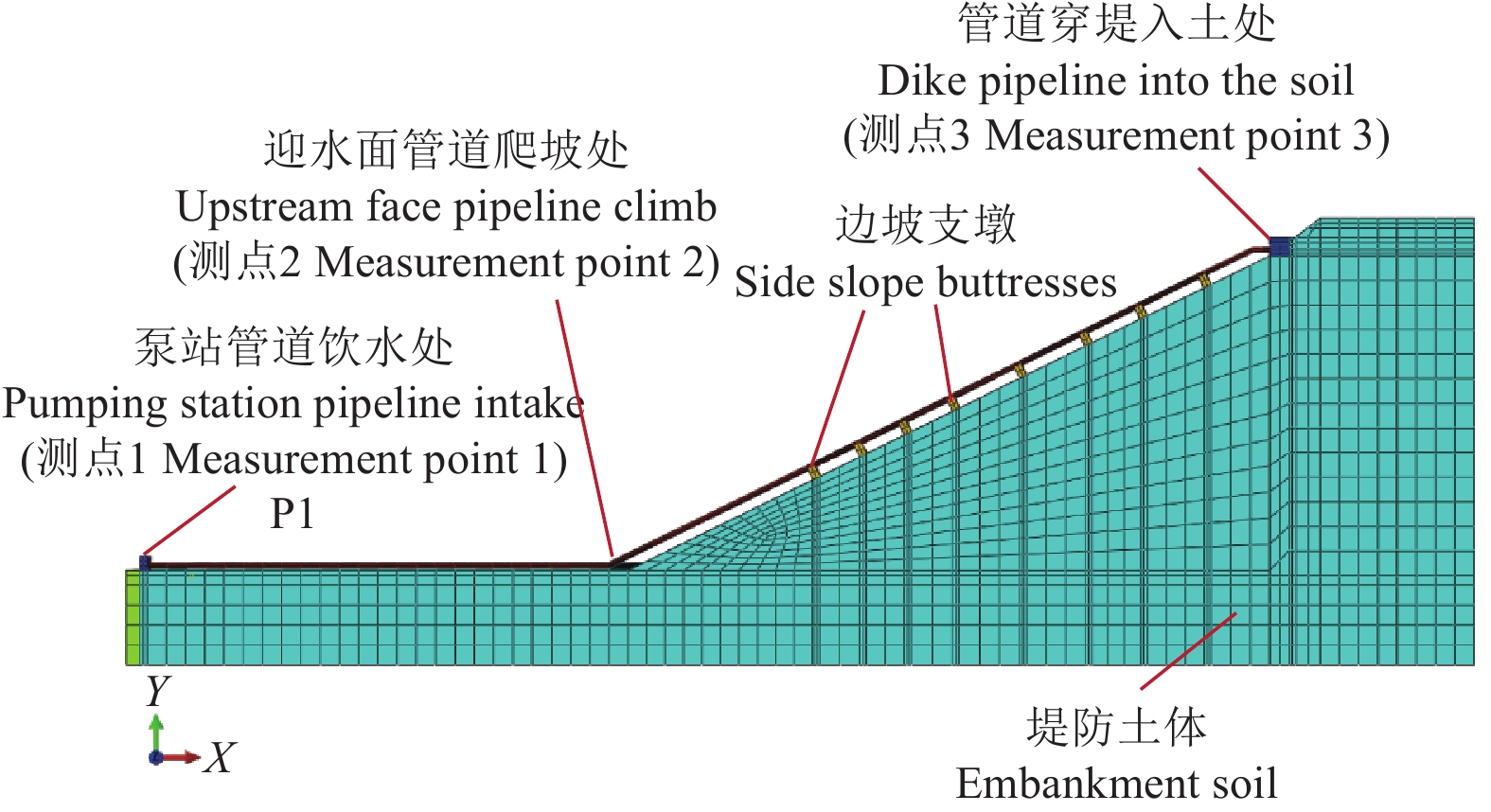
根据北江大堤穿堤管道尺寸参数，在ABAQUS中建立管道模型如图7所示，内径250 mm，外径270 mm，密度为7850 kg/m3，泊松比为0.3。由于管道爬坡段有较多边墩支墩，爬坡后管道振动响应相对较小，因此，本文在进行荷载反演建模时，仅针对测点1至测点2段管道建立二自由度模型。首先，根据现场采集得到的结构振动响应，利用荷载反演[25-27]方法得到管道振动等效荷载时程，将等效荷载时程自上而下施加在管道模型测点1处，得到测点1、测点2处位移为x1=7.05×10−7 m、x2=4.33×10−7 m。其次，根据模型位移计算出管道系统的刚度(N/m)矩阵$ {\boldsymbol{K}} = \left( {\begin{array}{*{20}{c}} {1.42 \times {{10}^6}}&0 \\ 0&{2.31 \times {{10}^6}} \end{array}} \right)$，采用Rayleigh阻尼确定阻尼矩阵$ {\boldsymbol{C}} $。最后建立北江大堤管道MRTMD混合控制振动动力方程。Rayleigh阻尼计算公式为[24]
$$ {\boldsymbol{C}} = {a_0}{\boldsymbol{M}} + {a_1}{\boldsymbol{K}} $$ (9) 式中，$ {a_0} $、$ {a_1} $为比例系数，取$ {a_0} = 0.0592 $、$ {a_1} = 0.0041 $，$ {\boldsymbol{M}} $为管道的二自由度质量(kg)矩阵，$ {\boldsymbol{M}} = \left( {\begin{array}{*{20}{c}} {1218}&0 \\ 0&{1218} \end{array}} \right)$。
3.2 结果与分析
为直观分析混合控制系统对穿堤管道振动减振控制效果，对比同一测点减振前后加速度和位移响应。MRTMD减振得到减振前后管道测点1、2的加速度和位移响应的均方根值与减振效率见表3。由表3可知，在测点1处布置MRTMD后，不仅能有效减小该处振动响应，而且还可以降低测点2处无控状态下的管道振动响应，MRTMD对测点1、2处加速度的减振效率分别为37.56%、38.07%，对测点1、2处位移的减振效率分别为40.23%、41.38%。
表 3 测点1、2处管道振动响应均方根值与减振效率Table 3. Root mean square value of pipeline vibration response and vibration reduction efficiency at measurement points 1 and 2测点
Measured points减振前
Before vibration reductionMRTMD 减振效率
Vibration reduction efficiency/%加速度
Acceleration/(mm·s−2)位移
Displacement/mm加速度
Acceleration/(mm·s−2)位移
Displacement/mm加速度
Acceleration位移
Displacement1 120.69 0.69 75.36 0.41 37.56 40.23 2 70.27 0.28 43.51 0.17 38.07 41.38 大量有关水轮机及泵站管道的研究表明，引起结构振动的主要原因有水力因素、机械因素和电气因素[28-30]。其中，水力因素包括：水流流经管道导致的低频水流脉动；叶轮内形成的轴向漩涡产生的中低频振动，一般在10 Hz左右。机械因素主要表现为：机组主轴的转频及其倍频；叶轮与隔舌耦合振动造成的中高频振动。
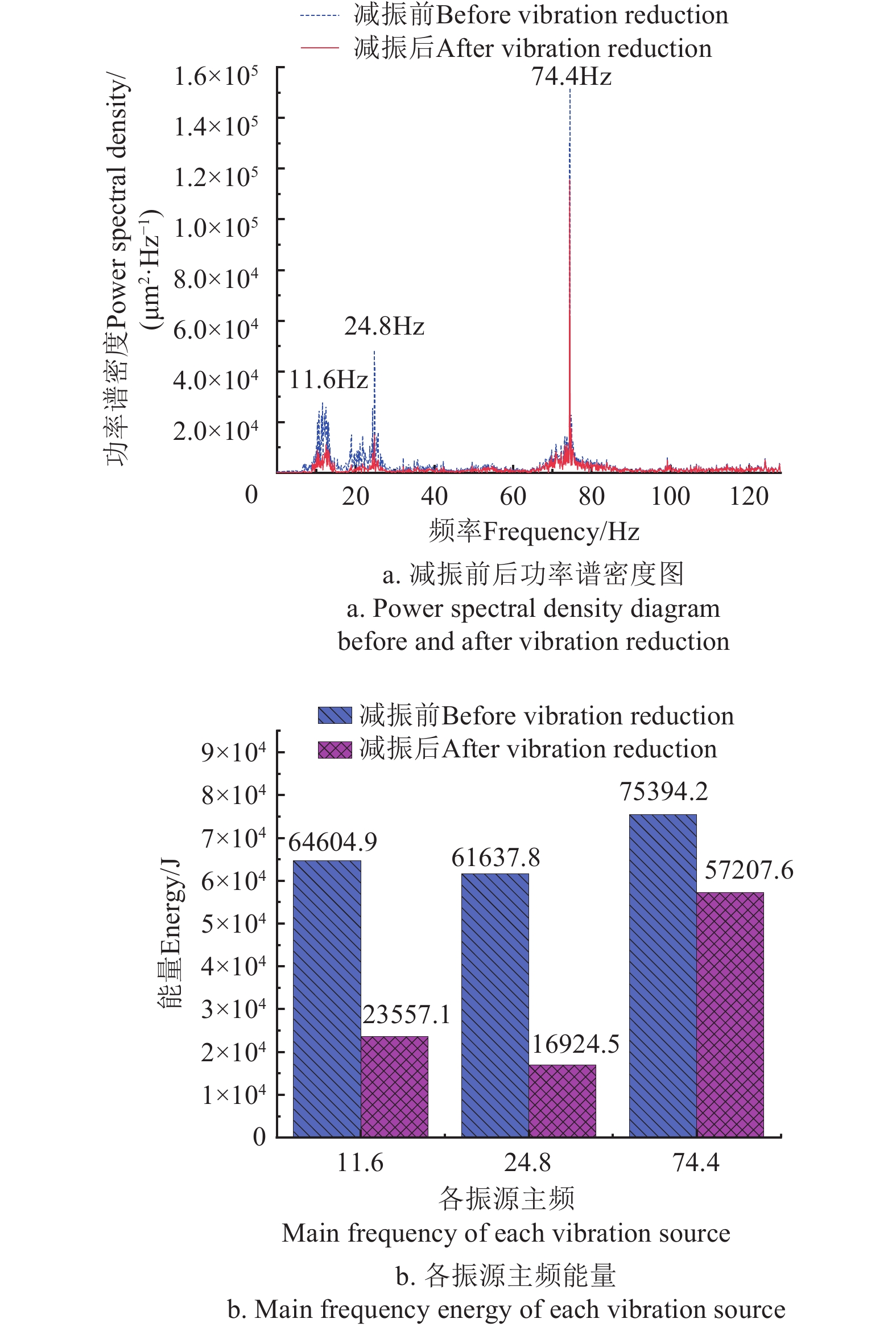
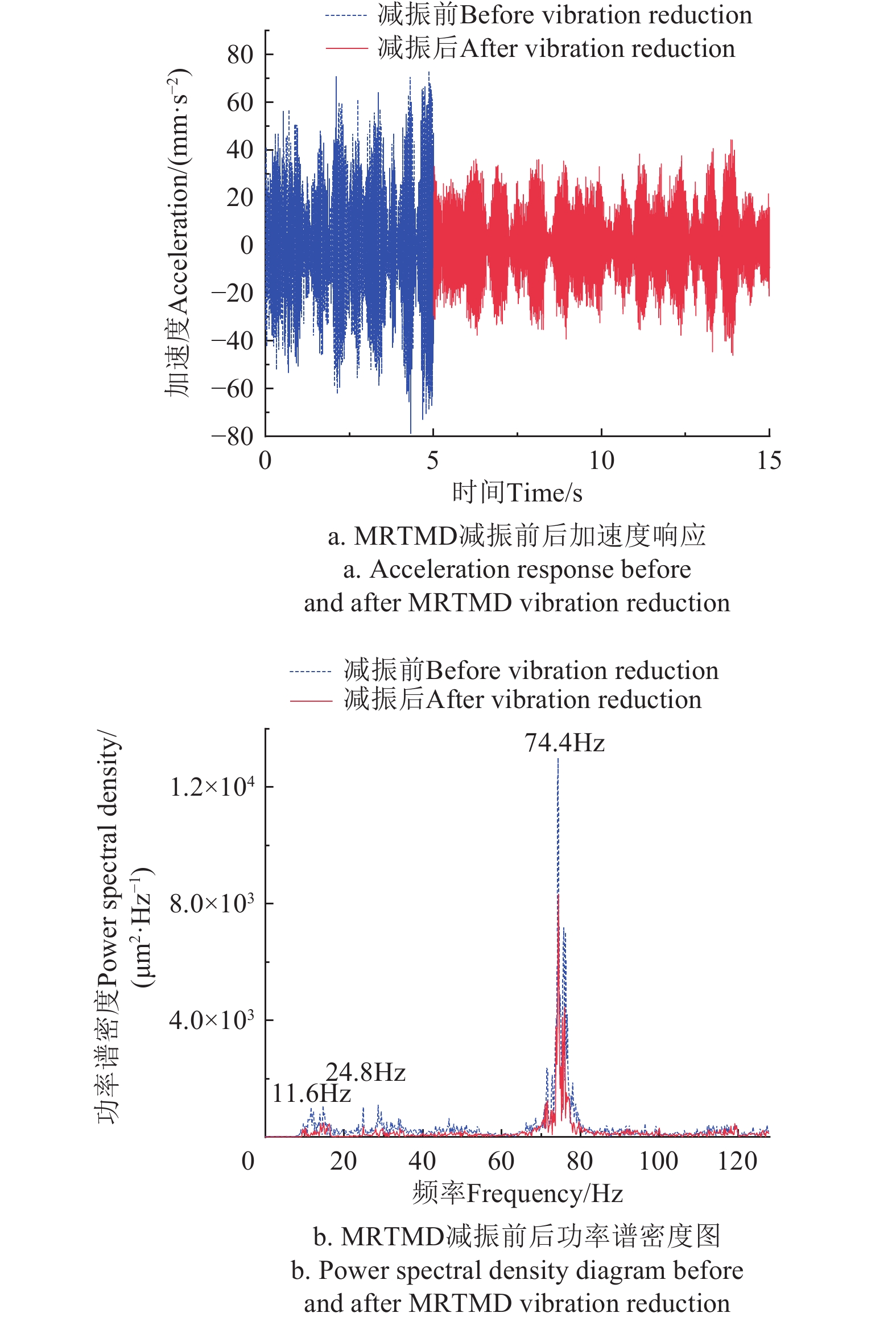
对减振前后的振动信号进行频谱分析，提取引起供排水穿堤管道振动的振源组成和优势频率，经过转速计算，造成穿堤管道振动的主要原因为泵站机组运行过程中的转频(24.8 Hz)及其三倍频(74.4 Hz)，其中74.4 Hz频率对应的幅值最大，为管道振动的主频；24.8 Hz频率对应的幅值次之，为次频；叶轮内形成的轴向漩涡造成的振动频率主要集中在11.6 Hz左右。对测点1进行频谱分析，得到MRTMD对管道振动主频、次频的减振效果，减振前后管道响应的功率谱密度与各振源主频能量如图8所示。
![]()
图 8 减振前后管道响应功率谱密度与各振源主频能量Figure 8. The power spectral density of pipeline response before and after vibration reduction and main frequency energy of each vibration source由图8可知，管道振动主频功率谱密度峰值由1.52×105 μm2/Hz降至1.16×105 μm2/Hz，能量降低至无控状态的75.88%；次频功率谱密度峰值由4.84×104 μm2/Hz降至1.50×104 μm2/Hz，能量降低至无控状态的27.46%；轴向漩涡造成的11.6 Hz振动频率的功率谱密度峰值由2.77×104 μm2/Hz降至1.10×104 μm2/Hz，能量降低至无控状态的36.46%。说明MRTMD对机组倍频、转频和中低频均有减振效果，减振频带范围广，尤其对水流脉动和轴向漩涡等中低频造成的振动有更明显的减振效果。
将MRTMD布置在测点1、2处，机组运行过程中有规律的开启、关闭MRTMD控制装置，在测点3处仅布置拾振器，采集该处管道振动响应，验证MRTMD对激励变化时的自适应减振能力。从关闭到开启MRTMD装置过程中测点3处管道振动加速度响应与功率谱密度如图9所示，由于穿堤处的大地脉动对管道振动的影响，开启前后的减振效率为33.9 %，略小于测点1、2布置MRTMD处的效率。由此可见，在振源激励较大的泵站机组处布置多自由度MRTMD混合控制装置，能大幅减小穿堤处的振动响应，削弱振动对堤防的影响，增加机组运行过程中的安全性。
![]()
图 9 测点3处振动加速度响应与功率谱密度Figure 9. Vibration acceleration response and power spectral density at measurement point 34. 结 论
1）本文提出磁流变MRD和调谐质量阻尼器TMD融合的MRTMD主被动混合控制装置，采用数值仿真分析验证该振动控制系统的有效性。结果表明，谐波激励作用下，MRTMD使结构加速度和位移响应减小37.26%和39.85%，响应峰值分别降低至无控状态下的40.20%和53.17%；冲击荷载作用下，结构加速度和位移响应减小30.51%和39.46%，响应峰值分别降低至无控状态下的70%和71%。
2）将MRTMD应用于穿堤管道原型试验，结果表明，MRTMD可针对激励变化自适应调整出力，对结构位移响应的控制效果略优于对加速度的控制效果，对结构加速度响应的控制效果达到37.56%～38.07%，位移响应的控制效果达到40.23%～41.38%，对管道穿堤前的减振效果达到33.9%，阻尼器响应迅速。机组倍频、转频和轴向漩涡造成的中低频振动能量分别减弱至无控状态的75.88%、27.46%和36.46%。
3）提出的融合磁流变阻尼器MRD与调谐质量阻尼器TMD的MRTMD主被动混合控制装置切实可行。装置采用LQR主动控制算法，MRTMD提供的阻尼力稳定，对结构的振动能量耗能能力较好，减振频带范围广，减振效果优于单一的TMD和MRD控制。
-
![]()
图 2 不同控制方法下结构加速度和位移响应对比(谐波)
Figure 2. Comparison of structural acceleration and displacement response under different control methods (harmonic)
![]()
图 4 不同控制方法下结构加速度和位移响应对比(冲击荷载)
Figure 4. Comparison of structural acceleration and displacement response under different control methods (shock excitation)
![]()
图 6 北江大堤穿堤管道现场图与剖面图
Figure 6. On site and cross-sectional view of the pipeline crossing the Beijiang embankment
![]()
图 8 减振前后管道响应功率谱密度与各振源主频能量
Figure 8. The power spectral density of pipeline response before and after vibration reduction and main frequency energy of each vibration source
![]()
图 9 测点3处振动加速度响应与功率谱密度
Figure 9. Vibration acceleration response and power spectral density at measurement point 3
表 1 谐波激励下结构响应均方根值及减振效率
Table 1 Root mean square value and vibration reduction efficiency of structural response under harmonic excitation
减振措施
Vibration
reduction
measures响应均方根值
Root mean square of response减振效率
Vibration reduction efficiency加速度Accelaration/
(mm·s−2)位移Displacement/
mm加速度Accelaration/
%位移Displacement/
%无控(减振前) 21.14 0.08 / / TMD 19.30 0.07 8.71 9.50 MRD 14.79 0.06 30.07 32.19 MRTMD 13.26 0.05 37.26 39.85 
下载: 导出CSV
表 2 冲击荷载激励下结构响应均方根值及减振效率
Table 2 Root mean square value and vibration reduction efficiency of structural response under shock wave excitation
减振措施
Vibration
reduction
measures响应均方根值
Root mean square of response减振效率
Vibration reduction efficiency加速度Accelaration/
(mm·s−2)位移Displacement/
mm加速度Accelaration/
%位移Displacement/
%无控(减振前) 5.76 2.4×10−2 − − TMD 5.22 2.1×10−2 9.34 13.19 MRD 4.42 1.7×10−2 23.30 30.37 MRTMD 4.00 1.4×10−2 30.51 39.46
下载: 导出CSV
表 3 测点1、2处管道振动响应均方根值与减振效率
Table 3 Root mean square value of pipeline vibration response and vibration reduction efficiency at measurement points 1 and 2
测点
Measured points减振前
Before vibration reductionMRTMD 减振效率
Vibration reduction efficiency/%加速度
Acceleration/(mm·s−2)位移
Displacement/mm加速度
Acceleration/(mm·s−2)位移
Displacement/mm加速度
Acceleration位移
Displacement1 120.69 0.69 75.36 0.41 37.56 40.23 2 70.27 0.28 43.51 0.17 38.07 41.38
下载: 导出CSV
-
[1] 张巧玲,黄铋匀,杨振东,等. 基于特征线法的含气输水管道水锤特性分析[J]. 农业工程学报,2022,38(5):79-86. ZHANG Qiaoling, HUANG Biyun, YANG Zhendong, et al. Water hammer properties of gas-bearing water pipeline using characteristics method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(5): 79-86. (in Chinese with English abstract)
[2] 汪怡然,俞晓东,韩笑笑,等. 考虑泥沙颗粒影响的长距离供水工程单向塔水锤防护[J]. 农业工程学报,2023,39(4):84-91. WANG Yiran, YU Xiaodong, HAN Xiaoxiao, et al. One-way surge tank protection of sediment-laden water hammer on long-distance water supply projects[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(4): 84-91. (in Chinese with English abstract)
[3] 王正中,江浩源,王羿,等. 旱寒区输水渠道防渗抗冻胀研究进展与前沿[J]. 农业工程学报,2020,36(22):120-132. WANG Zhengzhong, JIANG Haoyuan, WANG Yi, et al. Research progresses and frontiers in anti-seepage and anti-frost heave of canals in cold-arid regions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(22): 120-132. (in Chinese with English abstract)
[4] 司乔瑞,唐亚静,甘星城,等. 立式管道泵进水弯管和叶轮的参数化分析与验证[J]. 农业工程学报,2020,36(17):54-63. SI Qiaorui, TANG Yajing, GAN Xingcheng, et al. Parametric analysis and verification of curved inlet pipe and impeller of vertical inline pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(17): 54-63. (in Chinese with English abstract)
[5] 赵雷雷,于曰伟,曹建虎,等. 减振器节流阀片区段均布压力下应力解析算法及其应用[J]. 农业工程学报,2022,38(18):72-80. ZHAO Leilei, YU Yuewei, CAO Jianhu, et al. Analytical algorithm for the stress of damper throttle-slices and its application under interval uniformly distributed pressure[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(18): 72-80. (in Chinese with English abstract)
[6] ADDALA M B, BHALLA S, MADAN A. Performance based design of a new hybrid passive energy dissipation device for vibration control of reinforced concrete frames subjected to broad-ranging earthquake ground excitations[J]. Advances in Structural Engineering, 2022, 25(4): 895-912. DOI: 10.1177/13694332211052350
[7] 白久林,李晨辉,王宇航. 考虑RNA运行作用的近海风电结构主动质量阻尼器振动控制研究[J]. 振动与冲击,2023,42(23):183-191. BAI Jiulin, LI Chenhui, WANG Yuhang. Active mass damper vibration control of offshore wind turbine structure considering RNA operation[J]. Journal of Vibration and Shock, 2023, 42(23): 183-191. (in Chinese with English abstract)
[8] LIN Y F, VENNA S V. A novel method for piezoelectric transducers placement for passive vibration control of geometrically non‐linear structures[J]. Sensor Review, 2008, 28(3): 233-241. DOI: 10.1108/02602280810882599
[9] PORFIRI M, DELLISOLA F, SANTINI E. Modeling and design of passive electric networks interconnecting piezoelectric transducers for distributed vibration control[J]. International Journal of Applied Electromagnetics and Mechanics, 2005, 21(2): 69-87. DOI: 10.3233/JAE-2005-672
[10] PARK C H, PARK H C. Multiple-mode structural vibration control using negative capacitive shunt damping[J]. Journal of Mechanical Science and Technology, 2003, 17(11): 1650-1657.
[11] 杨毅,冷鼎鑫,徐凯,等. 磁流变调谐质量阻尼器在海上风机振动控制中的应[J]. 重庆大学学报,2022,45(3):20-30. YANG Yi, LENG Dingxin, XU Kai, et al. Application of magnetorheological TMD in vibration control of offshore wind turbines[J]. Journal of Chongqing University, 2022, 45(3): 20-30. (in Chinese with English abstract)
[12] XUE X, TANG J. Vibration control of nonlinear rotating beam using piezoelectric actuator and sliding mode approach[J]. Journal of Vibration and Control, 2008, 14(6): 885-908. DOI: 10.1177/1077546307085354
[13] QIU J H, HARAGUCHI M. Vibration control of a plate using a self-sensing piezoelectric actuator and an adaptive control approach[J]. Journal of Intelligent Material Systems and Structures, 2006(17): 660-669.
[14] 刘彦辉,谭平,周福霖,等. 主被动调谐控制结构动力响应分析与试验[J]. 振动、测试与诊断,2015,35(3):441-447, 587-588. LIU Yanhui, TAN Ping, ZHOU Fulin, et al. Experimental and analytical study of dynamic response of structure controlled by active-passive hybrid tune mass damper[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3): 441-447, 587-588. (in Chinese with English abstract)
[15] 廖英英,刘永强,杨绍普. 一种新型混合半主动控制策略在高速铁道车辆振动控制中的应用[J]. 振动与冲击,2013,32(12):84-87. LIAO Yingying, LIU Yongqiang, YANG Shaopu. A new mixed semi-active control strategy and its application in vibration control of a high-speed railway vehicles[J]. Journal of Vibration and Shock, 2013, 32(12): 84-87. (in Chinese with English abstract)
[16] 周亚丽,张奇志,熊斌. 基于分支电路的主动-被动混合式结构振动控制[J]. 噪声与振动控制,2006,5(6):5-8. ZHOU Yali, ZHANG Qizhi, XIONG Bin. Active-passive hybrid structural vibration control using shunted circuit[J]. Noise and Vibration Control, 2006, 5(6): 5-8. (in Chinese with English abstract)
[17] 马小陆,裘进浩,季宏丽,等. 负电容在主-被动混合压电振动控制中的应用[J]. 华南理工大学学报(自然科学版),2012,40(3):112-118. MA Xiaolu, QIU Jinhao, JI Hongli, et al. Application of negative capacitance to active-passive hybrid piezoelectric vibration control[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(3): 112-118. (in Chinese with English abstract)
[18] 赵祥昇,李春祥,曹黎媛. 结构-NFVD-TTMDI的控制性能[J]. 振动工程学报,2022,35(1):55-63. ZHAO Xiangsheng, LI Chunxiang, CAO Liyuan. Control performance of structural-NFVD-TTMDI[J]. Journal of Vibration Engineering, 2022, 35(1): 55-63. (in Chinese with English abstract)
[19] 张延年,刘斌,李艺,等. MRD与LRB相混合的结构振动控制[J]. 东北大学学报(自然科学版),2006,27(1):95-98. ZHANG Yannian, LIU Bin, LI Yi, et al. Structural vibration control using a mixture of MRD and LRB[J]. Journal of Northeastern University(Natural Science), 2006, 27(1): 95-98. (in Chinese with English abstract)
[20] 王海军,陈波,杨秀维,等. 抽水蓄能电站管道水力振动在围岩中的传播规律研究[J]. 水资源与水工程学报,2023,34(3):116-122. WANG Haijun, CHEN Bo, YANG Xiuwei, et al. Propagation law of hydraulic vibration of pipeline in surrounding rock of pumped storage power station[J]. Journal of Water Resources & Water Engineering, 2023, 34(3): 116-122. (in Chinese with English abstract)
[21] KHAZAEE M, KHADEM S E, MOSLEMI A, et al. Vibration mitigation of a pipe conveying fluid with a passive geometrically nonlinear absorber: A tuning optimal design[J]. Communications in Nonlinear Science and Numerical Simulation, 2020, 91(12): 105439.
[22] BORGI S E, ALRUMAIHI S, RAJENDRAN A, et al. Model updating of a scaled piping system and vibration attenuation via locally resonant bandgap formation[J]. International Journal of Mechanical Sciences, 2021, 194(11): 106211.
[23] 张翌娜,王立彬,张建伟,等. 梯级泵站管道TMD振动控制仿真与减振优化[J]. 水电能源科学,2018,36(8):153-157. ZHANG Yina, WANG Libin, ZHANG Jianwei, et al. Vibration control simulation and damping optimization of TMD system for pipeline of cascade pumping stations[J]. Water Resources and Power, 2018, 36(8): 153-157. (in Chinese with English abstract)
[24] 欧进萍. 结构振动控制-主动、半主动与智能控制[M]. 北京:科学出版社,2003:186-235. [25] 李火坤,杜磊,梁萱,等. 基于原型振动测试的泄洪闸闸墩动位移反演[J]. 振动、测试与诊断,2018,38(6):1122-1129, 1288. LI Huokun, DU Lei, LIANG Xuan, et al. Dynamic displacement inversion for sluice pier based on prototype vibration test[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(6): 1122-1129, 1288. (in Chinese with English abstract)
[26] 李火坤,王刚,魏博文,等. 基于敏感性分析与粒子群算法的拱坝原型动弹性模量反演方法[J]. 水利学报,2020,51(11):1401-1411. LI Huokun, WANG Gang, WEI Bowen, et al. Inversion of prototype dynamic elastic modulus of arch dam based on sensitivity analysis and particle swarm optimization[J]. Journal of Hydraulic Engineering, 2020, 51(11): 1401-1411. (in Chinese with English abstract)
[27] 张建伟,崔广涛,马斌,等. 基于泄流响应的高拱坝振源时域识别[J]. 天津大学学报(自然科学与工程技术版),2008,41(9):1124-1129. ZHANG Jianwei, CUI Guangtao, MA Bin, et al. Time domain identification of excitation sources for high arch dams based on discharge flow vibration response[J]. Journal of Tianjin University(Science and Technology), 2008, 41(9): 1124-1129. (in Chinese with English abstract)
[28] 张建伟,江琦,王涛. 基于原型观测的梯级泵站管道振源特性分析[J]. 农业工程学报,2017,33(1):77-83. DOI: 10.11975/j.issn.1002-6819.2017.01.010 ZHANG Jianwei, JIANG Qi, WANG Tao. Analysis of vibration characteristics of pipeline of trapezoid pumping station based on prototype observation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(1): 77-83. (in Chinese with English abstract) DOI: 10.11975/j.issn.1002-6819.2017.01.010
[29] 张龑,练继建,刘昉,等. 基于原型观测的厂顶溢流式水电站厂房结构振动特性研究[J]. 天津大学学报(自然科学与工程技术版),2015,48(7):584-590. ZHANG Yan, LIAN Jijian, LIU Fang, et al. Vibration characteristics of powerhouse structure of roof overflow hydroelectric station based on prototype observation[J]. Journal of Tianjin University(Science and Technology), 2015, 48(7): 584-590. (in Chinese with English abstract)
[30] 张建伟,杨灿,黄锦林,等. 基于传递熵的泵站管道振动传递路径特性分析[J]. 农业工程学报,2021,37(15):47-52. ZHANG Jianwei, YANG Can, HUANG Jinlin, et al. Analysis of the pipeline transfer path characteristics of pumping stations based on transfer entropy[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(15): 47-52. (in Chinese with English abstract)
-
期刊类型引用(0)
其他类型引用(3)
计量
- 文章访问数: 0
- HTML全文浏览量: 1
- PDF下载量: 0
- 被引次数: 3
下载:
