Research on fertilizer application strategy for rice-wheat dual-variable precision fertilizer applicator based on MLP
-
摘要:
变量施肥是实施精准农业的重要技术途径，转速、开度双重调节的外槽轮式变量施肥方式是稻麦轮作区作物施肥的典型方式。针对目前变量施肥机控制系统响应速度慢、预测模型不准确，引起排肥量误差大、成效不显著的问题，该研究基于自主研制的稻麦双变量精准施肥机，运用数理统计和机器学习方法，提出一种基于多层感知人工神经网络的排肥量预测模型，并对其有效性和适用性进行验证。通过分析莱维飞行算法(levy flight algorithm, LFA)、粒子群算法(particle swarm optimization, PSO)和多层感知器神经网络模型(multilayer perceptron, MLP)的算法机理，结合开度-转速双变量排肥方法，构建LFA-PSO-MLP排肥量预测模型；引入开度-转速-排肥量关系模型，利用归一化、正则化等方式改善算法结构，开展参数优化和模型训练，并对比MLP和PSO-MLP模型，得到LFA-PSO-MLP排肥量最优预测模型；构建ILMP（inverse LFA-PSO-MLP）预测模型作为施肥机的神经网络模型，根据目标排肥量快速计算所需开度和转速。试验结果表明：LFA-PSO-MLP模型在拟合50次左右收敛，拟合500次后的R2值为0.999，平均相对误差(MAPE)为1.83%，均优于其他两种模型。LMP验证集验证试验中，预测值和验证值比的平均相对误差为2.47%，田间试验的预测值和实测值比的平均相对误差为3.49%；ILMP验证试验中，转速预测的平均相对误差为1.82%，目标排肥量与实际排肥量比的最大相对误差为7.22%，平均排肥精度达到93.92%，施肥机排肥效果较好。所提模型能够在保证排肥量预测精度的同时提升运算效率，实现快速、精准、高效的变量施肥，改善生态效益和经济效益。
Abstract:Variable fertilization is an important technical approach in implementing precision agriculture. The method of external groove wheel-type variable fertilization with dual regulation of speed and aperture is a typical operation method for crop production (planting) in rice-wheat rotation areas. In response to current issues with variable fertilizer applicators such as slow control system response, inaccurate prediction models, large fertilizer amount errors, and insignificant effectiveness, this study, based on a self-developed dual-variable precision fertilizer applicator for rice and wheat, proposed a method for constructing a fertilizer amount prediction model based on a multilayer perceptron artificial neural network using mathematical statistics and machine learning methods, and verified its effectiveness and applicability. By analyzing the algorithm mechanisms of the levy flight algorithm (LFA), particle swarm optimization (PSO), and multilayer perceptron (MLP) neural network models, and combining the dual-variable fertilization method of aperture-speed, a fertilizer amount prediction model based on LFA-PSO-MLP (LMP) was constructed. The model incorporated the aperture-speed-fertilizer amount relationship, improved algorithm structure through normalization, regularization, etc., conducted parameter optimization and model training, and compared the MLP and PSO-MLP models to obtain the optimal LFA-PSO-MLP fertilizer amount prediction model. Furthermore, an inverse LFA-PSO-MLP (ILMP) prediction model was constructed to quickly calculate the required aperture and speed based on the target fertilizer amount. Experimental results showed that the LFA-PSO-MLP model converged in about 50 iterations, with an R² value of 0.999 after 500 iterations and a mean absolute percentage error (MAPE) of 1.83%, which was better than the other two models. Validation tests of the LMP model yielded an average relative error of 2.47% between predicted and validation values, while field experiments showed an average relative error of 3.49% between predicted and measured values. For the ILMP model, the average relative error for rotation speed prediction was 1.82%, and in field experiments, the maximum relative error between target and actual fertilization rates was 7.22%, with an average fertilization accuracy of 93.92%. This indicated that the fertilizer applicator equipped with the ILMP model performed well in fertilizer application. The study demonstrated that the proposed model construction method can ensure the accuracy of fertilizer amount prediction while improving computational efficiency, achieving fast, precise, and efficient variable fertilization, and improving ecological and economic benefits.
-
0. 引 言
水稻、小麦等粮食作物在生产过程中对常量和微量元素的需求量在不同区域、尺度、时期下不完全相同，因此按需变量施肥技术在现代农业发展进程中应运而生，为推动精准农业可持续发展提供了一种有效的技术途径[1]。变量施肥技术能够根据作物生长状况、土壤条件和环境等因素精准确定每个区域或单元的施肥量需求，最大限度地提高施肥效率和作物产量[2-3]。外槽轮式变量施肥作为长江中下游稻麦轮作区作物种植常用的典型基肥、追肥作业方式[4-6]，为避免其单一变量控制的缺点，如开度变化导致肥料碰撞溅射，或转速变化导致排肥脉动变化等，将开度和转速设置为排肥量调节的双重变量，以提高外槽轮式排肥器排肥调节的准确性和稳定性。
实现排肥量精准调节的关键在于对排肥器的开度和转速做快速、科学、合理、有效的控制[7]。排肥器开度、转速和排肥量之间存在非线性关系[8]，三者的关系模型较为复杂，但是排肥量预测对于高效生产、成本节约、环境保护、资源设置优化以及农业决策等均有较大裨益[9]，所以基于排肥器开度和转速的排肥量预测模型构建成为农业科学研究的重点内容之一。现有预测模型的构建方法主要是统计模型[10]、机器学习[11]、深度学习[12]和基于GIS与遥感技术的空间预测[13]。其中，统计模型方法简单易懂、适应性强，但受限于自身的模型特征，不能很好地表达非线性关系；机器学习方法对复杂数据和非线性关系的处理效果普遍较好，但需要大量数据作为支撑，且计算时间较长；深度学习方法在处理复杂特征和关系的能力更强，但需要的数据规模庞大，且计算时间相比机器学习普遍更长，效率较低；空间预测方法可以综合运用多种数据进行建模，但获取数据成本较高。
贾海峰等[14]运用云计算技术分析玉米土壤养分含量关系，利用优化神经网络技术建立与分析玉米土壤养分施肥模型，研究表明构建的FCM-OLS-RBF（fuzzy C-means, ordinary least squar, radial basis function）施肥量预测模型与传统RBF模型相比精度明显提高，预测性能更好；杨烁楠等[15]以6种环境信息作为辅助，借助OK（ordinary kriging）、RF（random forest）、RFRK（random forest with residual kriging）三种预测模型对土壤有机质空间分布进行预测，划分施肥分区，以此制定施肥方案，结果表明三种模型对土壤有机质的预测效果基本一致；黄珍等[16]基于神经网络模型构建玉米精准施肥模型，提出结合BP（back propagation）神经网络的施肥算法，对土壤养分含量和玉米产量进行分析研究，结果表明，结合BP神经网络的精准施肥模型的预测相对误差在0.1%左右，有较高的预测精度；张季琴等[17-18]基于灰狼算法和广义回归神经网络提出GWO-GRNN（grey wolf optimization, generalized regression neural network）排肥量预测模型，通过三种固体肥料颗粒开展排肥试验，并与现有DE-GRNN（differential evolution）模型进行对比，结果表明GWO-GRNN模型的收敛速度更快，运行时间更短，且对三种肥料颗粒的预测模型决定系数均在0.99以上，具有较高的预测效率；巩海亮[19]提出了基于归一化植被指数的玉米中耕变量施肥预测调控模型，分析玉米冠层NDVI（normalized difference vegetation index），引入自适应三次指数预测算法得出NDVI预测值，再结合施肥优化算法，实现对施肥量的调控，结果表明该模型可以较好地完成区域施肥量的实时计算。可以看出，现有研究主要集中在对作物种植目标施肥量预测模型的关注，且大多是针对单变量的目标控制方法。针对稻麦变量施肥机排肥量预测，尤其是开度和转速双变量调控的研究较少，无法满足稻麦精确变量施肥的要求。
为此，本文以课题组前期研制的外槽轮式稻麦双变量精准施肥机[7, 20]为基础，结合莱维飞行算法（levy flight algorithm, LFA）和粒子群优化（particle swarm optimization, PSO）算法，提出一种经LFA优化与PSO寻优的MLP(multilayer perceptron)前馈神经网络模型，配合近地光谱检测等技术，对稻麦双变量精准施肥机的排肥量做正、反向预测，并进行试验验证,以提高排肥效率，改善施肥机的作业精度，提高作业性能。
1. 整体结构与工作原理
1.1 整体结构
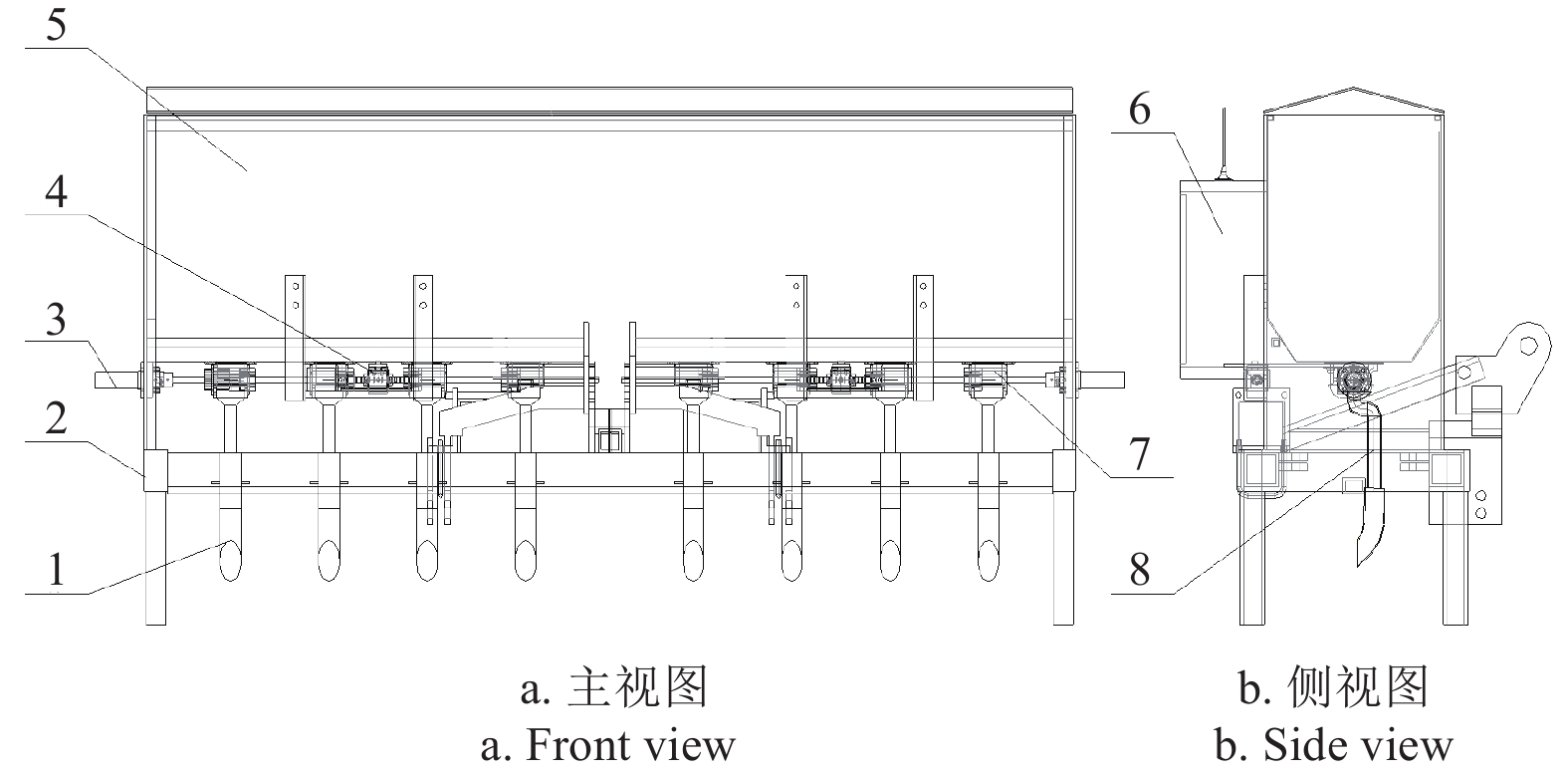
前期课题组自主研发的稻麦双变量精准施肥机的整机结构如图1所示，主要由传感器、车载计算机、测控系统、排肥系统、行走系统和各配合装置等部分组成。施肥机整体采用轴分段式设计，设置排肥器8 个，以 4 个为一组共配备独立系统2组，工作幅宽各1 m，可以分别调整开度和转速。同组的排肥器由同一施肥传动轴带动，为控制转速，在传动轴的一端连接无刷直流行星减速电动机；为控制开度，将丝杆螺母由 2 相 4 线行星减速步进电动机进行驱动。直流电动机额定功率为 100 w，减速后的额定转速为 100 r/min，扭矩为 12 N·m；步进电动机额定扭矩为 29.4 N·m。整机的作业幅宽为2 m，适用于小地块作业；排肥器由阻塞轮、排肥槽轮、排肥轴、排肥盒以及落种壳等部件组成[21]，排肥槽轮外径为58 mm，排肥口直径为41 mm。施肥机上配有蓄电池组，为工作部件供电。
![]()
图 1 稻麦双变量精准施肥机1.排肥口 2.机架总体 3.直流行星减速电动机 4.行星减速步进电动机 5.肥料箱 6.控制箱 7.排肥器 8.排肥管Figure 1. Rice-wheat dual-variable precision fertilizer applicator1.Fertilizer Discharge Port 2.Overall Frame 3.DC Planetary Gear Reduction Motor 4.Planetary Gear Reduction Stepper Motor 5.Fertilizer Box 6.Control Box 7.Fertilizer Dispenser 8.Fertilizer Discharge Tube1.2 工作原理
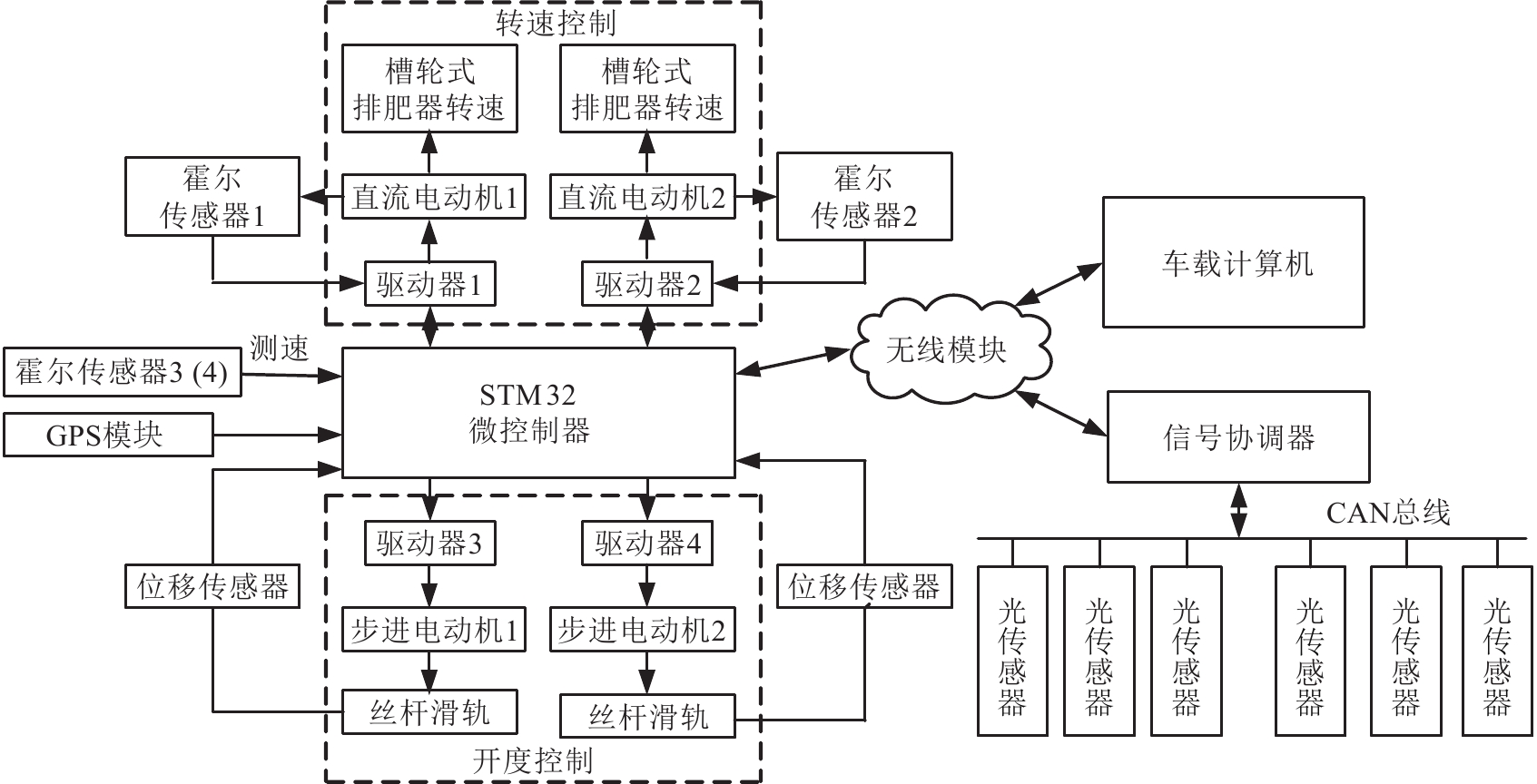
双变量精准施肥机工作原理如图2所示。
近地光谱传感器检测作物冠层归一化植被指数（NDVI），将数据传输给车载计算机，后者启动变量施肥专家决策系统，结合当前行进速度和位置信息，依据内嵌的Raun施肥模型实时生成目标排肥量，并发送给ILMP模型作为参数输入。ILMP模型根据目标排肥量对排种器的开度-转速参数组合做实时计算，将其处理为控制指令，并通过无线串口发送给控制器，调节排肥执行机构（电机），同时传感器在线采集排肥器转速、开度信息，形成对稻麦精准变量施肥的闭环控制。
2. 基于LFA-PSO-MLP算法的排肥量预测模型
2.1 粒子群优化算法原理
粒子群优化算法[22-23]（particle swarm optimization, PSO）中的每个粒子代表一个潜在解，并在解空间中迭代移动。在迭代过程中，粒子的移动受到个体最优力和社会最优力的影响。粒子的速度和位置根据这两种力进行更新，直到达到停止条件。
对于第i个粒子，其速度更新公式为
$$ \boldsymbol{\mathbf{\boldsymbol{v}}}_i^{(t+1)}=\omega\cdot\boldsymbol{v}_i^{(t)}+c_1\cdot r_1^{ }\cdot(P_i^{(t)}-\boldsymbol{x}_i^{(t)})+c_2\cdot r_2^{ }\cdot(P_g^{(t)}-\boldsymbol{x}_i^{(t)}) $$ (1) 式中vi(t+1)是第i个粒子在下一次迭代中的速度；vi(t)是第i个粒子在当前迭代中的速度；ω是惯性权重；c1和c2分别代表个体学习因子和社会学习因子；r1和r2是[0, 1]的随机数；Pi(t)是第i个粒子在当前迭代中的个体最优位置；Pg(t)是整个粒子群在当前迭代中的全局最优位置；xi(t)是第i个粒子在当前迭代中的位置。
根据新的速度，第i个粒子的位置xi在每一次迭代更新中变化如下：
$$ \boldsymbol{x}_i^{(t+1)}=\boldsymbol{x}_i^{(t)}+\boldsymbol{v}_i^{(t+1)} $$ (2) 式中xi(t+1)是第i个粒子在下一次迭代中的位置。
尽管粒子群算法自身的全局优化能力较强，但该算法对粒子数量、惯性权重和加速系数等参数较敏感，候选解在拟合过程中易剧烈抖动或陷入局部最优解；同时算法特性导致粒子间信息共享过于密集，这也会使粒子群在局部聚集，陷入局部最优。本文引入莱维飞行算法优化粒子的移动策略，以提高粒子在搜索空间中移动的随机性和多样性，增强全局搜索和寻优能力。
2.2 莱维飞行算法原理
莱维飞行算法[24-25](levy flight algorithm, LFA)模拟动物在搜索过程中的随机性和长距离跳跃的特性搜索空间并找到最优解。
莱维飞行算法通过莱维分布产生随机步长，其长尾性质的概率密度函数为
$$ p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\mathrm{e}^{-\frac{1}{2}(\frac{1}{x})^{\frac{1}{\beta}}} $$ (3) 式中σ为尺度参数；β为形状参数。
根据生成的随机步长更新当前位置，更新公式为
$$ \boldsymbol{x}_{new}=\boldsymbol{x}_{old}+\alpha\cdot Levy $$ (4) 式中xnew是粒子的新位置；xold是粒子的当前位置；ɑ是控制步长的缩放参数；Levy是具有长尾特性的概率分布。
通过结合LFA算法的随机游走特性和PSO算法的群体智能特性，可以有效改善粒子的移动策略，使粒子的移动方式更加随机化和多样化，脱离只依赖当前速度和加速度的传统移动方式，改善算法的搜索能力，使其在拟合过程中快速收敛，不仅能够大幅减小粒子移动时的剧烈抖动，还可降低算法陷入局部最优解的可能性，增强算法的全局搜索能力，提高算法解决复杂问题时的鲁棒性和适应性。
2.3 多层感知器前馈神经网络模型原理
多层感知器[26-29]（multilayer perceptron, MLP）前馈神经网络算法通过尝试模拟神经元之间的连接和信息传递过程，实现对数据的学习和预测。
假设有一个单层的 MLP，其中有一个输入层和一个输出层。输入层有n个神经元，输出层有m个神经元。每个神经元都与上一层的每个神经元相连，则输入层到隐藏层的计算中，对于第j个隐藏层神经元，输入的加权求和计算式为
$$ {{\textit{z}}_j} = \sum\limits_{i = 1}^n {{w_{ij}} \cdot {x^{{'}}}_i + {b_j}} $$ (5) 式中zj是隐藏层神经元的输入加权求和；wij是输入层与隐藏层之间的权重；xi'是输入层的第i个神经元的输出；bj是隐藏层神经元的偏置。
将加权求和结果应用到激活函数f(zj)，便得隐藏层神经元的输出为
$$ {a_j} = f({{\textit{z}}_j}) $$ (6) 隐藏层到输出层的计算中，对于输出层的每个神经元k，输入的加权求和计算式为
$$ {{\textit{z}}_k} = \sum\limits_{j = 1}^m {{w_{jk}} \cdot {a_j} + {b_k}} $$ (7) 式中zk是输出层神经元的输入加权求和；wjk是隐藏层与输出层之间的权重；aj是隐藏层的第j个神经元的输出；bk是输出层神经元的偏置。
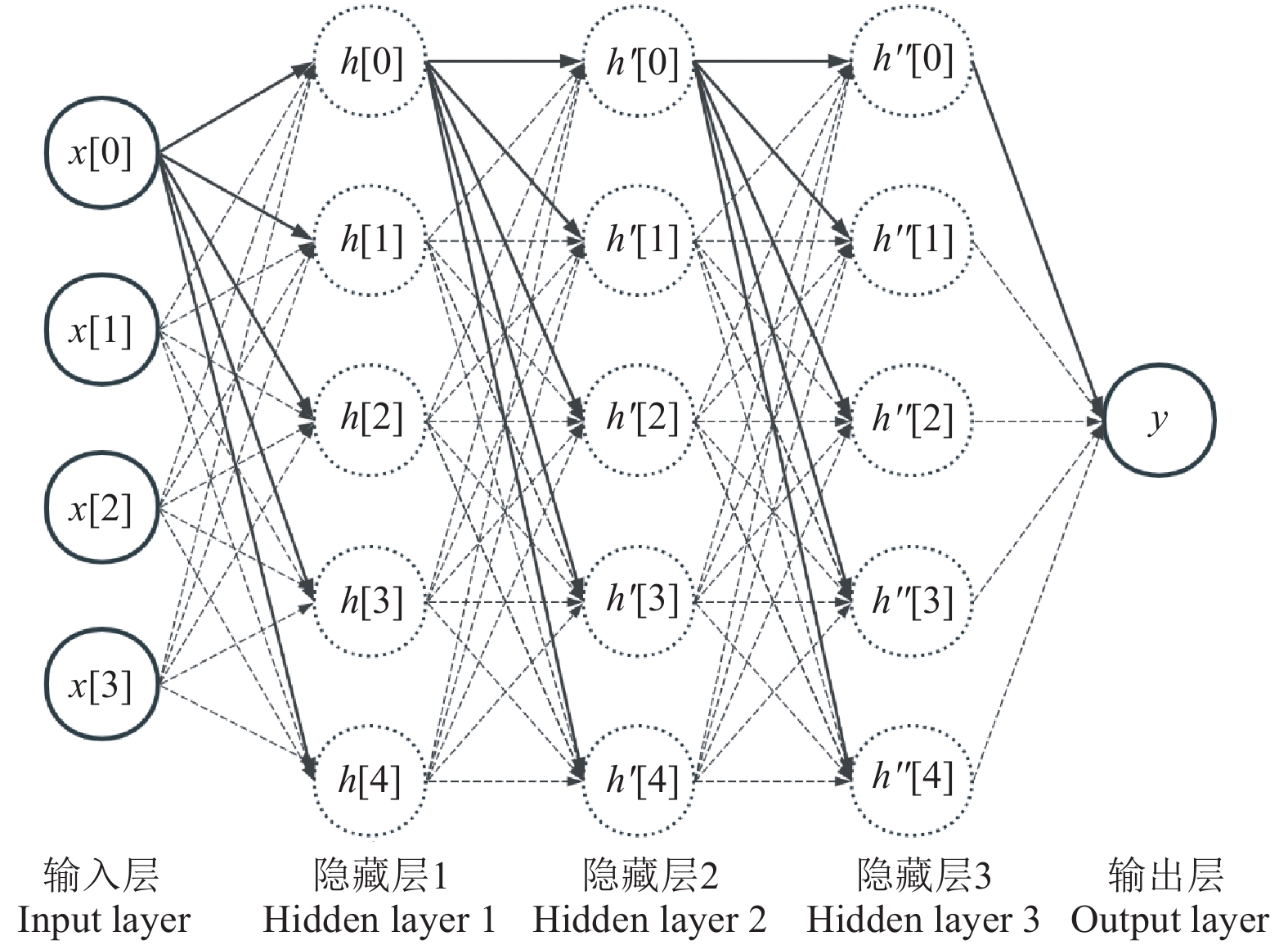
最后，将加权求和结果应用于输出层的激活函数，得到输出层神经元的输出。从单一隐藏层拓展到多个隐藏层，其过程为从输入层到隐藏层，以及隐藏层之间各自对输入做加权、偏置和通过激活函数生成本层输出，再作为输入传递给各自的下一个结构层，最终得到输出层的结果。MLP模型的网络结构如图3所示。
![]()
图 3 MLP模型结构注：x[0]~x[3]为输入层的4个输入特征；h[0]~h[4]、h´[0]~h´[4]及h´´[0]~h´´[4]分别为各层前一个节点经线性组合输入与激活函数处理后生成的输出；y为模型的总输出。Note: x[0]-x[3] represents the four input features of the input layer; h[0]-h[4], h'[0]-h'[4], and h''[0]-h''[4] represent the outputs generated by the linear combination of inputs and the activation function processing of each layer's previous node, respectively; y represents the overall output of the model.Figure 3. Structure of multilayer perceptron（MLP）2.4 LFA-PSO-MLP排肥量预测模型构建
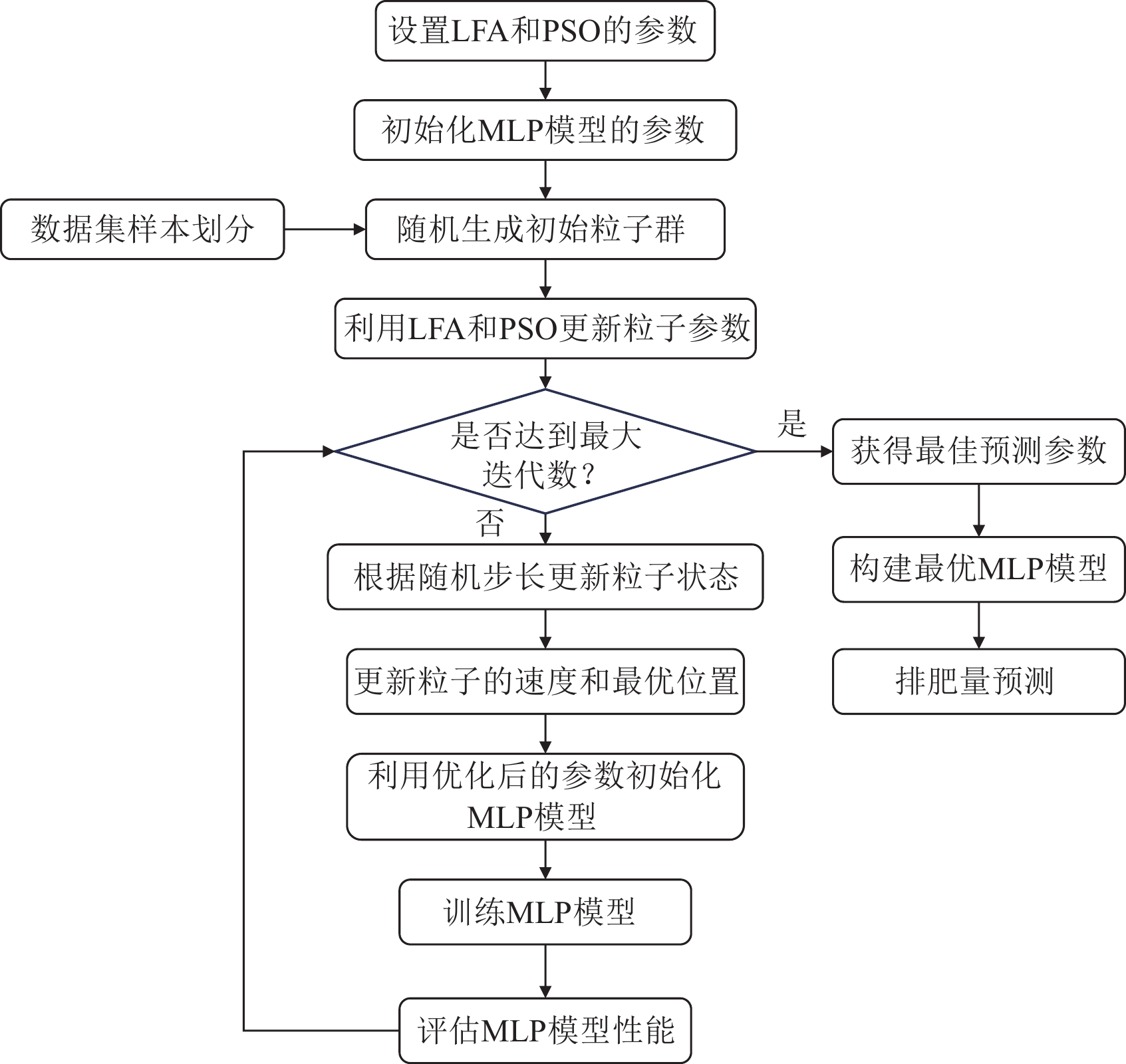
模型算法实现流程如图4所示，具体包括算法参数设置、数据集准备、算法优化、模型优化和模型测试。首先设置LFA、PSO和MLP各自的初始化参数，再将训练集和测试集按照一定比例划分，并做数据归一化处理，消除量纲影响，降低特征值的偏重性；更新PSO粒子个体的特征参数，再运用LFA对粒子的位置和速度进行更新，得出最佳预测参数，引入并训练MLP模型，加入L2正则，提高模型泛化能力，避免模型过拟合，最终得到排肥量最优预测模型。
![]()
图 4 LFA-PSO-MLP算法流程Figure 4. Flowchart of levy flight algorithm-particle swarm optimization-multilayer perceptron algorithm3. 排肥量标定试验
以长江中下游稻麦轮作区常用颗粒复合肥[30-31]为对象，颗粒直径为3.98 mm，其他物料特性参数如表1所示，在南京农业大学工学院智能化农业机械实验室进行排肥量标定试验（如图5所示），使用的排肥器为自研双变量排肥器[21]。
表 1 物料特性参数Table 1. Material characteristic parameters参数
Parameters颗粒
Particle槽轮
Grooved wheel地面
Ground钢材
Steel泊松比 0.24 0.47 0.51 0.3 剪切模量/MPa 10.76 0.95 1.10×102 7×104 密度/(×103kg·m−3) 1.38 1.06 1.25 7.80 接触力学参数 名称
Name颗粒-颗粒
Particle-particle颗粒-槽轮
Particle-grooved wheel颗粒-地面
Particle-ground颗粒-钢材
Particle-steel弹性恢复因数 0.27 0.35 0.06 0.29 动摩擦因数 0.26 0.32 1.2 0.59 静摩擦因数 0.34 0.47 1.13 0.48 3.1 试验条件
排肥口开度调节范围20 ～45 mm，调节步长5 mm；排肥轴转速调节范围20 ～60 r/min，调节步长5 r/min，共54种开度-转速组合，试验变量编码水平如表2所示，每组试验时长1 min，3次重复，结果取平均值。
表 2 试验变量编码水平表Table 2. Experimental variable encoding level table编码值
Coded value排肥器开度
Opening L/mm排肥器转速
Speed N/(r·min−1)−1 20 20 1 45 60 3.2 排肥量响应曲线与残差分布
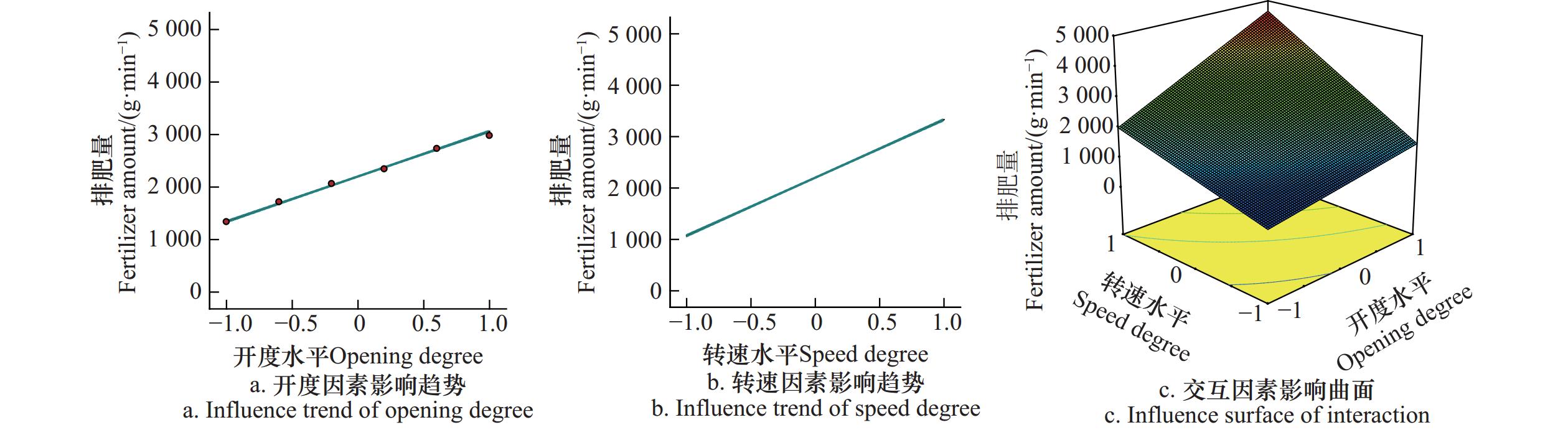
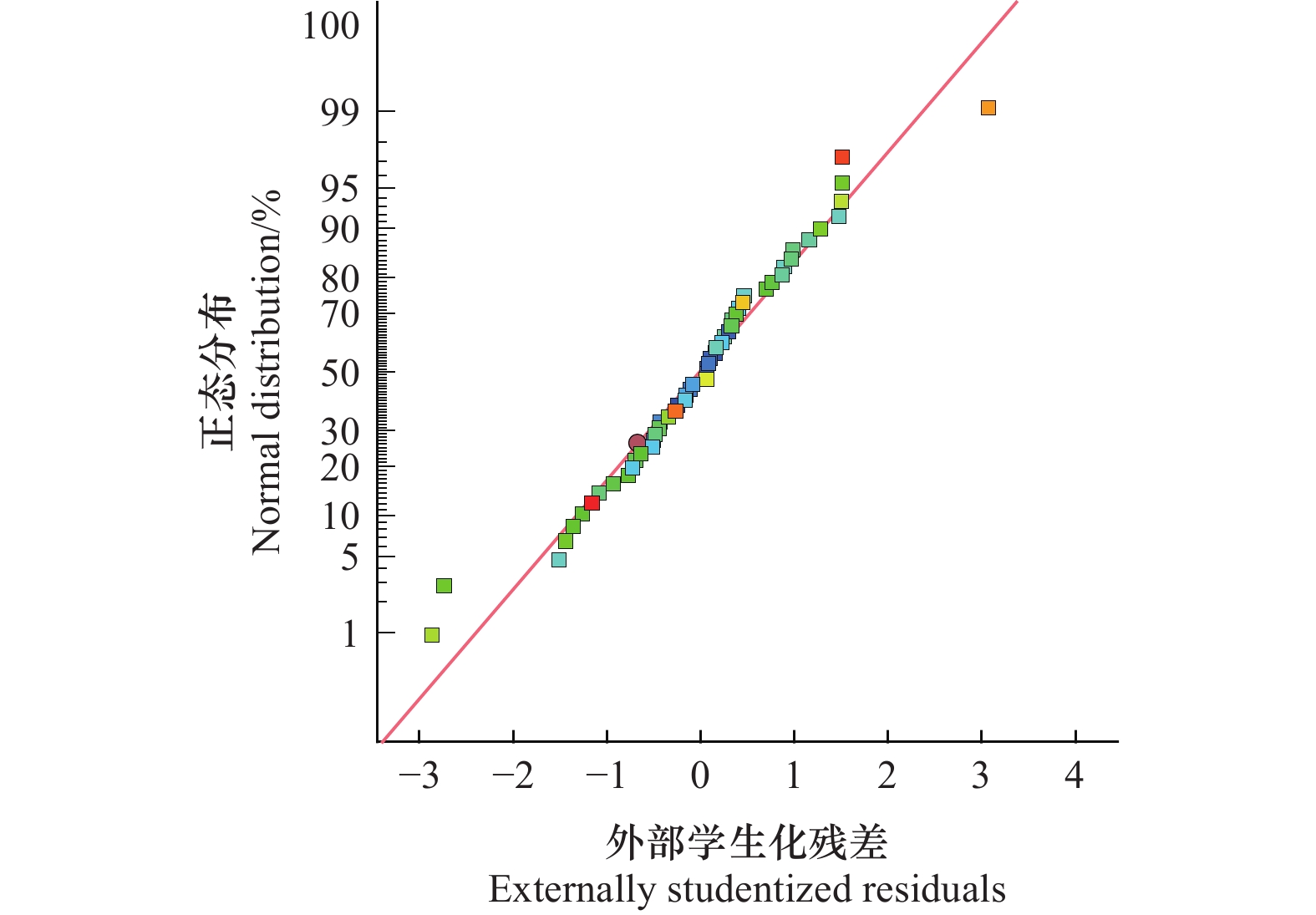
运用Design-expert10.0.1软件分析试验数据，建立排肥器开度-转速-排肥量关系模型，单因素影响曲线和交互因素影响曲面如图6所示，外部学生化残差正态分布如图7所示。
![]()
图 6 单因素和交互因素对排肥量的影响Figure 6. Effects of single and interaction factors on fertilizer distribution3.2.1 排肥量响应曲线与曲面分析
从图6可以看出，排肥量随开度和转速的增大而增大，其中排肥量最小值和最大值分别出现在开度和转速的−1和1水平，且转速对排肥量的影响大于开度；而开度和转速的交互作用对排肥量的影响大于单因素的影响，排肥量最小值和最大值分别出现在−1和1的交互水平，为656.48和
4 606.55 g/min。3.2.2 外部学生化残差分析
外部学生化残差(externally studentized residuals, ESR)是一种用于检测异常值的方法。在线性回归分析中将残差除以标准误差，产生外部学生化残差，用以对异常值进行检测。数据的外部学生化残差的绝对值大于3为异常值，小于2可用于分析。从图7中可看出，54种开度-转速组合产生的排肥量数据中有3组的残差绝对值接近3，其他51组数据的残差绝对值均处于[0, 2]范围内，说明标定试验效果较好，可作为排肥量标定参考。
4. LFA-PSO-MLP模型的构建与参数优化
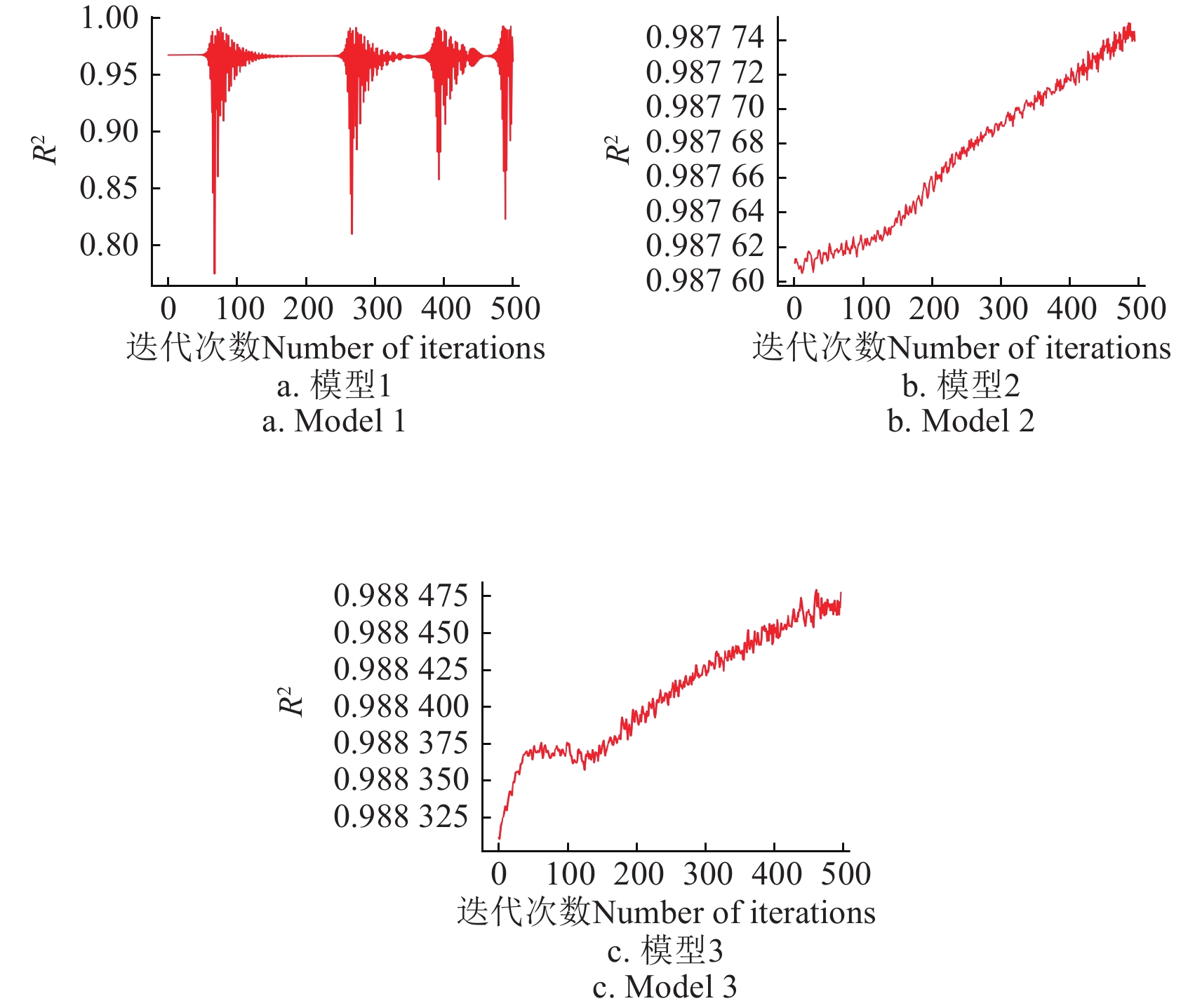
本文LFA-PSO-MLP模型算法的运行环境为Intel(R) Core(TM) i5-9300H CPU @ 2.40 GHz，内存16 G，操作系统为64位Windows10，软件为Visual-Studio-Code 1.88.1。根据2.4节方法初步建立LFA-PSO-MLP模型，初始化参数方面，设置PSO中的粒子数量为10，初始位置为[0.05, 0.05]，最大迭代次数为100；LFA的莱维飞行参数为1.5，飞行步长范围为[0, 0.1]，惯性权重为1.0，学习因子均为1.0；MLP的最小学习率为0.001，最大迭代次数为500，训练得出的R2曲线如图8所示。
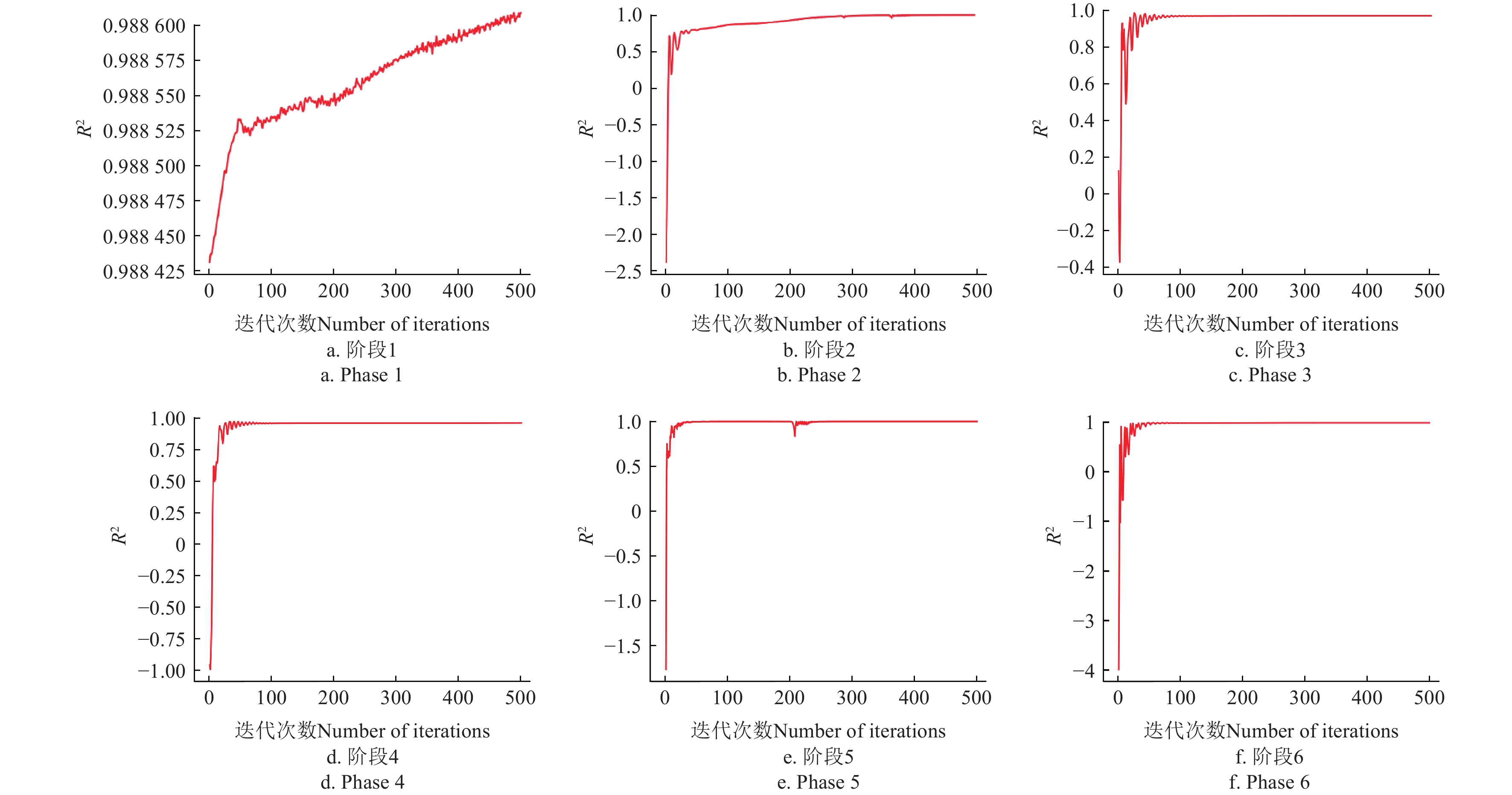
图8中，3次训练得到的对应模型的R2出现上下波动甚至跳出收敛域反转发散的情况，并且训练结束后得到的R2值较小，没有达到预期要求。这是因为惯性权重、学习率等相关初始化参数设置不合理，并且数据集缺乏规范化等。为此，通过不断调节初始化参数以及引入归一化、正则化等操作，得到LFA-PSO-MLP模型的R2递进优化结果如图9所示。
![]()
图 9 LFA-PSO-MLP模型的R2递进优化过程Figure 9. Progressive optimization process of R2 of LFA-PSO-MLP model由图9可知，随着迭代次数逐步逼近500，图9a至图9b的R2值逐渐上升但波动依旧较大，拟合不完全；图9c至图9d在迭代80次左右快速收敛，但R2值未逼近1，拟合程度不高；图9e至图9f在50代左右快速收敛，且R2值逼近1，实现高度拟合，符合预期要求。
5. 模型对比
为了验证LFA-PSO-MLP算法的合理性和有效性，本文将该模型与传统MLP模型、PSO-MLP模型分别做比较，从收敛性和拟合程度等方面进行模型分析和评价。
5.1 试验环境及参数设置
3种算法采用同一数据集进行训练与测试。采用205组试验数据，以排肥器的开度和转速为特征变量，排肥量为目标变量，以0.85:0.15设置训练集和测试集的数量；初始化参数方面，设置PSO粒子数量为10，（若其他模型中未出现则不设置），初始位置为[0.05, 0.05]，最大迭代次数为100；设置LFA中的莱维飞行参数为2，飞行步长范围为[0, 0.01]，惯性权重为0.5，学习因子均为1.5；设置MLP的最小学习率为
0.000 1 ，正则化参数为0.05，最大迭代次数为500。为避免与试验普遍效果偏差较大的小概率事件影响对试验结果的判断，3种模型各训练10次，每次均拟合500代，以出现次数比重极大的模型为最终试验结果。若与普遍效果相差较大的结果出现比例较大，则增加训练次数，确保模型训练的正确性和非偶然性。5.2 运行结果及分析
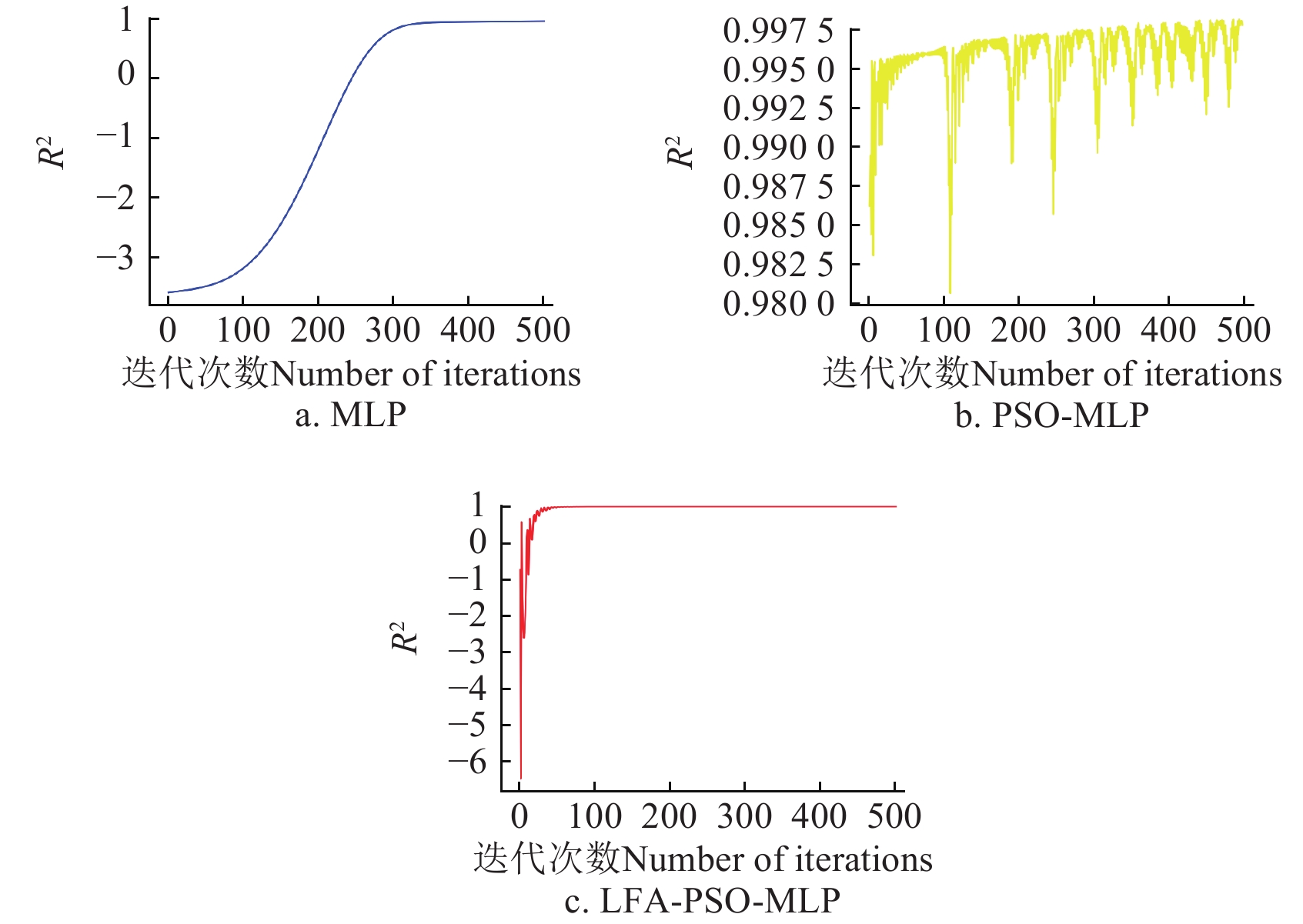
3种模型拟合过程中的R2收敛曲线如图10所示。
由图10可知，MLP模型的R2在100代内缓慢收敛，在100~300代快速收敛，并在300代后趋于1；PSO-MLP模型的R2在迭代中始终处于[0.975, 1]，但是波动较大，难以稳定收敛，这是因为MLP 的参数空间较大，且存在多个局部最优解，此时PSO 可能会在多个局部最优解之间跳跃，引起R2波动；本文LFA-PSO-MLP模型在迭代初始快速稳定收敛，0～50次迭代内迅速收敛，并在微小波动后趋于1。
各模型训练10次的稳定拟合代数和迭代500次时的R2以及平均相对误差（MAPE）等如表3所示。
表 3 模型训练的R2和MAPETable 3. R2 and mean absolute percentage error obtained from model training训练次数
Number of training iterationsMLP PSO-MLP LFA-PSO-MLP R2 MAPE R2 MAPE R2 MAPE 1 0.943 13.01 0.992 2.87 0.998 1.93 2 0.993 2.79 0.999 1.80 3 0.989 2.99 0.998 1.83 4 0.995 2.80 0.998 1.89 5 0.987 3.08 0.999 1.77 6 0.989 3.02 0.999 1.80 7 0.991 2.94 0.998 1.84 8 0.988 2.99 0.998 1.84 9 0.99 2.96 0.999 1.79 10 0.992 2.92 0.998 1.84 均值 0.988 2.95 0.999 1.83 稳定拟合代数 300 / 50 需要注意的是，MLP模型在通过本数据集做的10次训练中均于拟合500代前达到最佳状态，故R2和MAPE保持不变；而PSO-MLP和LFA-PSO-MLP模型在10次训练中均未在500代达到完全拟合。考虑在拟合到500代时2种模型的测试精度均较高，而增加拟合代数产生的时间代价远大于提升精度产生的收益，故本试验设定拟合代数最高为500。
5.2.1 模型的收敛性
图10中，MLP模型经历了从初始缓慢收敛，到拟合100次后逐步加速收敛，再到拟合300次后缓慢收敛并趋于稳定的过程；PSO-MLP模型的拟合曲线始终处于波动状态，难以达到收敛要求；而LFA-PSO-MLP模型经历了从初始快速波动式拟合，再到拟合50次后缓慢收敛并趋于稳定的过程。可见后者的响应速度、响应质量与稳定性均优于前两者，整体收敛表现更佳。
5.2.2 模型的拟合程度
表3中，在迭代500次结束后，MLP模型的R2为0.943，MAPE为13.01%，远大于其他两种模型；而后两者虽然差别较小，但LFA-PSO-MLP的R2比PSO-MLP减小了0.011，MAPE减小了1.12%。结合二者拟合时的波动状态，对比得出LFA-PSO-MLP的拟合程度优于PSO-MLP，即从整体拟合表现来看，LFA-PSO-MLP模型与其他两种模型相比拟合效果更佳。
综上所述，基于LFA-PSO-MLP的排肥量预测模型在收敛性和拟合程度方面均优于其他两种模型，在排肥量预测中具有更大的优势。因此本文采用LFA-PSO-MLP算法模型对基于排肥器开度和转速的排肥量预测模型进行构建。
5.3 基于LFA-PSO-MLP的排肥量预测模型分析
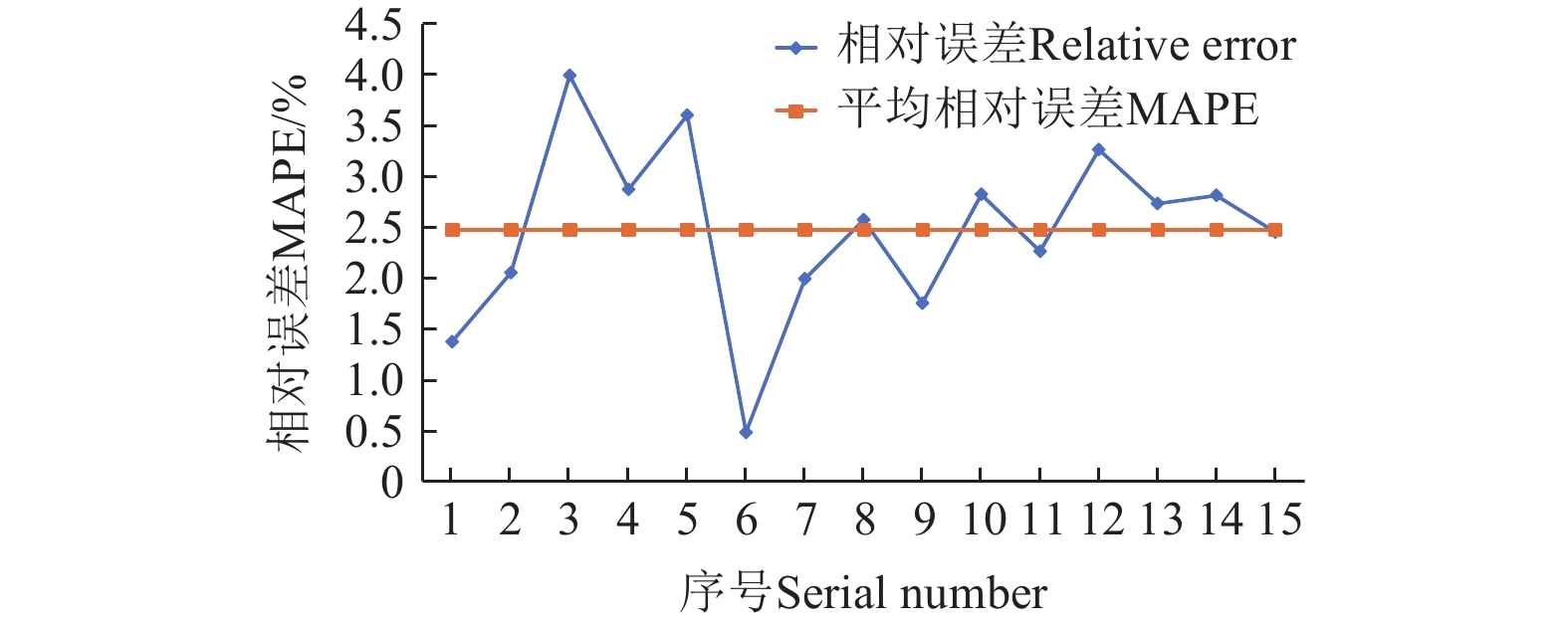
在得出排肥量模型的最优参数后，建立基于排肥器开度-转速的排肥量最优预测模型。为验证该预测模型的实用性和泛化能力，本文选用未参加训练的15组验证集，对预测模型做验证试验。计算模型的预测排肥量，并与验证集的排肥量作比较，利用MAPE对模型的拟合程度做进一步评价。验证值和预测值的对比数据如表4所示，相对误差如图11所示。
表 4 排肥量验证值与预测值的对比Table 4. Comparison between validation and predicted values of fertilizer application amounts序号
No.开度 Opening L/
mm转速 Speed N/
(r·min−1)验证值
Verification value Q/
(g·min−1)预测值
Predicted value P/(g·min−1)相对误差
Relative
error/%1 23 23 1020.438 1034.406 1.37 2 23 33 1390.638 1419.156 2.05 3 23 43 1751.322 1821.186 3.99 4 23 53 2151.618 2213.298 2.87 5 23 63 2504.772 2595.048 3.6 6 35 23 1435.152 1428.222 0.48 7 35 33 2044.548 2003.796 1.99 8 35 43 2627.13 2559.702 2.57 9 35 53 3212.91 3156.564 1.75 10 35 63 3829.41 3721.314 2.82 11 43 23 1866.858 1824.606 2.26 12 43 33 2642.034 2556.012 3.26 13 43 43 3415.578 3322.296 2.73 14 43 53 4182.63 4065.072 2.81 15 43 63 4911.174 4791.09 2.45 表4中，每个开度-转速组合对应的排肥量验证值和预测值之差均有上下浮动，其最大相对误差为3.99%，最小相对误差为0.48%，对应差值分别为69.86 g/min和6.93 g/min，平均相对误差为2.47%；总体上预测数据与验证数据的相对误差虽在0.5%～4%范围内波动，但整体波动并不明显。这说明LMP模型的预测精度较高，效果较好，符合对基于排肥器开度和转速的排肥量预测的要求，满足后续基于目标排肥量的开度-转速反向预测模型(inverse LFA-PSO-MLP)的构建条件。
6. 基于目标排肥量的排肥器开度与转速反向预测试验
为实现稻麦双变量精准施肥机检测、处理与实时控制一体化与自动化，针对光谱追肥检测系统与变量追肥决策系统等综合生成的目标排肥量，以LMP为基础模型，做排肥器开度与转速实时控制试验。运用Visual-Studio-Code 1.88.1软件，利用第5节LMP最优预测模型，编写基于目标排肥量的开度-转速反向预测模型(inverse LFA-PSO-MLP, ILPM)。
因以目标排肥量做开度-转速参数组合反向预测的结果不唯一，需针对不同目标排肥量做ILMP预测的梯度设计。参考文献[21]的方法，以转速优先控制策略为基础，将不同目标排肥量区间做排肥器开度梯度适应设计，每个区间对应一个开度，这样可以减少开度-转速参数组合无规则变化，大幅减小模型计算量，同时减少排肥波动，提高稳定性。为减小试验误差，以表4中9个验证值数据为反向预测的试验数据基础，设计目标排肥量梯度区间在[
1000 ,2500 ）时，开度为23 mm；[2500 ,4000 ）时开度为35 mm；[4000 ,5500 ）时，开度为43 mm，进行反向预测试验。试验结果如表5所示，转速参考值与预测值相对误差最大为2.52%，最小为1.06%，平均相对误差为1.82%，这说明ILMP模型可以较好地处理基于目标排肥量准确调节排肥器开度、转速组合的问题，为良好适配光谱追肥检测系统与变量追肥决策系统，实现稻麦双变量精准施肥机测控一体化做好理论基础。
表 5 ILMP模型预测结果Table 5. Result related to inverse prediction of the ILMP model序号
No.目标排肥量
Verification value Q/
(g·min−1)开度
Opening L /mm转速参考值
Reference value N/
(r·min−1)转速预测值
Predicted value Np/
(r·min−1)相对误差
Relative error /%1 1020.438 23 23 23.53 2.30 2 1390.638 23 33 32.48 1.58 3 1751.322 23 43 43.96 2.23 4 2151.618 23 53 54.01 1.91 5 2627.13 35 43 42.39 1.42 6 3212.91 35 53 53.64 1.21 7 3829.41 35 63 64.59 2.52 8 4182.63 43 53 54.12 2.11 9 4911.174 43 63 62.33 1.06 7. 试验验证
为验证LPM和ILMP模型的有效性和可行性，在江苏省东台五烈现代农业示范园使用课题组自主研发的稻麦双变量精准施肥机开展试验验证，试验如图12所示。
7.1 LFA-PSO-MLP排肥量预测试验
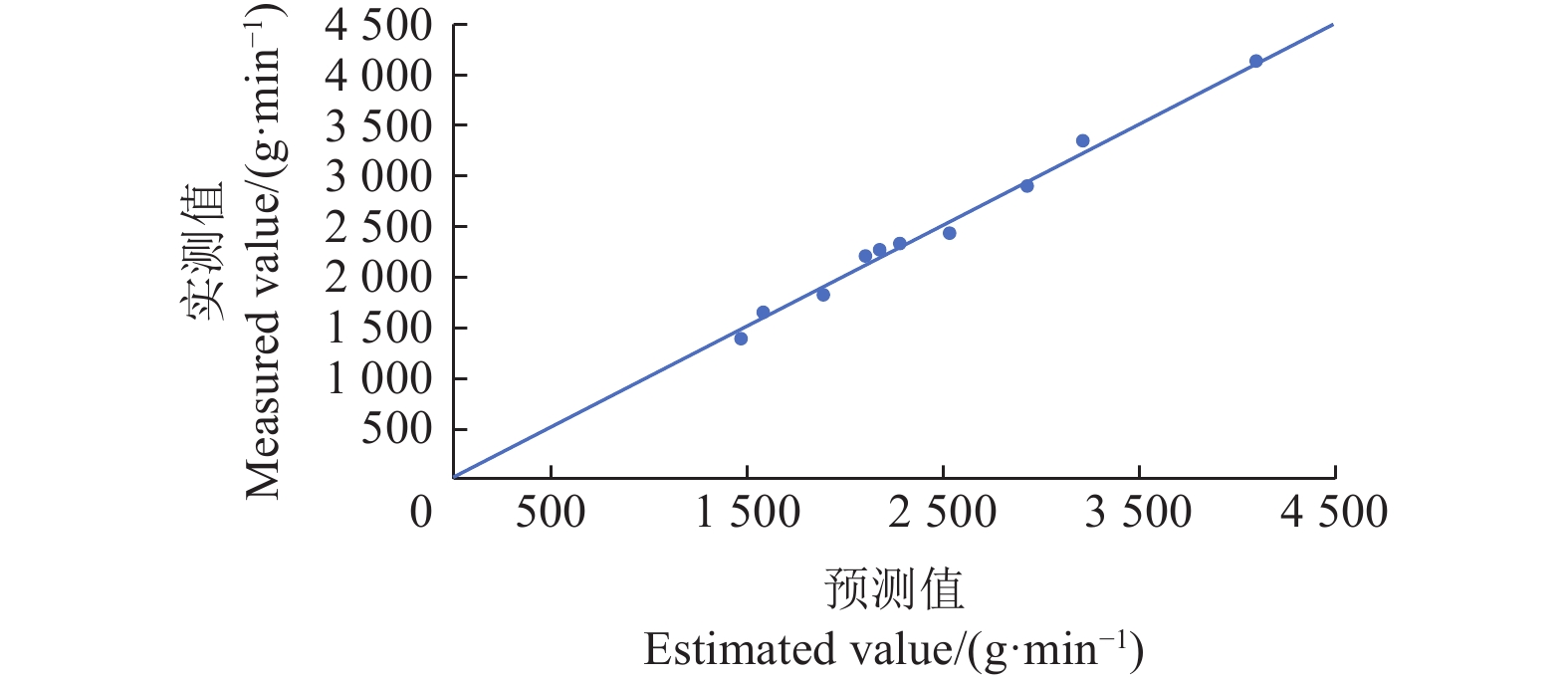
设定施肥机的行进速度为1 m/s，排肥器的开度范围为[20 ～45 mm]，转速范围为[20 ～60 r/min]；使用的肥料颗粒为南京正美实农化有限公司研制的复合肥料，进行基于开度和转速双变量下，时长为1 min的排肥试验共10次，记录每次排肥试验的开度、转速和排肥量实测值，并与LPM模型得出的排肥量预测值做对比，计算其与实测值的相对误差。经排肥试验得到的排肥量实测值和预测值以及相对误差如表6所示，LPM模型的排肥量预测性能如图13所示。
表 6 排肥量的实测值和预测值及其相关数据Table 6. Measured and predicted values of fertilizer distribution and their correlation data试验序号
No.开度
Opening转速组合
Speed combination排肥量实测值
Measured value /(g·min−1)排肥量预测值
Predicted value /(g·min−1)相对误差
Relative error/%1 25 30 1388.74 1466.27 5.59 2 25 40 1822.21 1886.69 3.54 3 25 50 2330.98 2276.31 2.35 4 30 30 1649.75 1580.16 4.22 5 30 40 2207.43 2101.32 4.81 6 30 50 2431.96 2531.3 4.08 7 40 30 2269.11 2173.96 4.19 8 40 40 2897.16 2926.71 1.02 9 45 40 3347.4 3210.62 4.09 10 45 50 4137.22 4094.76 1.03 ![]()
图 13 基于LFA-PSO-MLP模型的排肥量预测性能Figure 13. Fertilizer distribution prediction performance based on the LFA-PSO-MLP model表6中，在10种不同的开度-转速组合中，排肥量的实测值和预测值分别分布在
1388.74 ～4137.22 g/min和1466.27 ～4094.76 g/min范围内，均达到正常的排肥标准。且实测值和预测值的最大相对误差为5.59%；最小相对误差为1.02%；整体的平均相对误差为3.49%，相对误差较小，说明预测精度较高。图13表明试验验证的预测值与实际值均在排肥量的同一水平上下浮动，且差值较小，说明模型能够很好地拟合实际排肥情况。7.2 inverse LFA-PSO-MLP开度-转速预测试验
在验证LMP模型的可行性与有效性后，于园内进一步做搭载ILMP模型的施肥机排肥试验。本次试验中，施肥机以1 m/s的速度直线行走共6次，每次的作业面积为180 m2，测量并记录每次的目标排肥量和经ILMP模型实时调节开度与转速后得到的实际排肥量，以相对误差为评价指标，评价搭载ILMP模型后施肥机的排肥效果，试验结果如表7所示。
表 7 搭载ILMP模型的施肥机排肥结果Table 7. Fertilization results of the fertilizer applicator equipped with the ILMP model试验序号
Test No.目标排肥量
Target value/g实际排肥量
Measured value /g单位时间排肥量
Measured value per time/(g·min−1)相对误差
Relative error /%1 5612.93 5260.72 3507.15 6.70 2 5960.31 5605.16 3803.44 6.34 3 5821.91 5428.03 3752.02 7.26 4 5647.63 5293.44 3528.96 6.69 5 6064.18 5655.98 3770.65 7.22 6 5777.36 5645.73 3763.82 2.33 表7中，施肥机的目标排肥量与实际排肥量的相对误差普遍在[6.34%，7.26%]区间内，平均排肥精度为93.92%，精度较高，试验结果符合预期。这说明搭载ILMP模型的稻麦双变量精准施肥机的排肥效果较好，能够满足排肥作业要求。
8. 结 论
1）通过分析莱维飞行算法（levy flight algorithm, LFA）、粒子群算法（particle swarm optimization, PSO）的优化原理和多层感知器神经网络模型（multilayer perceptron, MLP）的构建机理，设计了嵌套算法技术路线，运用编程软件Visual-Studio-Code 1.88.1构建和优化了基于排肥器开度和转速的LFA-PSO-MLP排肥量预测模型以及基于目标排肥量的inverse LFA-PSO-MLP开度-转速预测模型。
2）对MLP、PSO-MLP和LFA-PSO-MLP三种模型的训练结果进行分析，结果表明LFA-PSO-MLP的R2在迭代过程中可快速达到0.999，平均相对误差为1.83%，均优于其他两种模型。开展验证集验证试验结果表明，模型预测值与验证集的验证值平均误差为2.47%；ILMP模型的验证试验平均相对误差为1.82%，预测精度高，试验效果较好。
3）结合稻麦冠层归一化植被指数(NDVI)检测技术，搭配多层感知机神经网络模型，构建稻麦双变量精准施肥机实时测控一体化系统。LMP田间试验中模型预测的平均相对误差为3.49%；ILMP田间试验模型预测的平均排肥精度为93.92%。说明该预测模型可以较好地针对目标排肥量快速、精准预测所需的开度和转速参数，完成精准农业高效变量施肥作业，实现对肥料资源的优化利用和对环境的保护，提升生态效益和经济效益。
-
![]()
图 1 稻麦双变量精准施肥机
1.排肥口 2.机架总体 3.直流行星减速电动机 4.行星减速步进电动机 5.肥料箱 6.控制箱 7.排肥器 8.排肥管
Figure 1. Rice-wheat dual-variable precision fertilizer applicator
1.Fertilizer Discharge Port 2.Overall Frame 3.DC Planetary Gear Reduction Motor 4.Planetary Gear Reduction Stepper Motor 5.Fertilizer Box 6.Control Box 7.Fertilizer Dispenser 8.Fertilizer Discharge Tube
![]()
图 3 MLP模型结构
注：x[0]~x[3]为输入层的4个输入特征；h[0]~h[4]、h´[0]~h´[4]及h´´[0]~h´´[4]分别为各层前一个节点经线性组合输入与激活函数处理后生成的输出；y为模型的总输出。Note: x[0]-x[3] represents the four input features of the input layer; h[0]-h[4], h'[0]-h'[4], and h''[0]-h''[4] represent the outputs generated by the linear combination of inputs and the activation function processing of each layer's previous node, respectively; y represents the overall output of the model.
Figure 3. Structure of multilayer perceptron（MLP）
![]()
图 4 LFA-PSO-MLP算法流程
Figure 4. Flowchart of levy flight algorithm-particle swarm optimization-multilayer perceptron algorithm
![]()
图 6 单因素和交互因素对排肥量的影响
Figure 6. Effects of single and interaction factors on fertilizer distribution
![]()
图 9 LFA-PSO-MLP模型的R2递进优化过程
Figure 9. Progressive optimization process of R2 of LFA-PSO-MLP model
![]()
图 13 基于LFA-PSO-MLP模型的排肥量预测性能
Figure 13. Fertilizer distribution prediction performance based on the LFA-PSO-MLP model
表 1 物料特性参数
Table 1 Material characteristic parameters
参数
Parameters颗粒
Particle槽轮
Grooved wheel地面
Ground钢材
Steel泊松比 0.24 0.47 0.51 0.3 剪切模量/MPa 10.76 0.95 1.10×102 7×104 密度/(×103kg·m−3) 1.38 1.06 1.25 7.80 接触力学参数 名称
Name颗粒-颗粒
Particle-particle颗粒-槽轮
Particle-grooved wheel颗粒-地面
Particle-ground颗粒-钢材
Particle-steel弹性恢复因数 0.27 0.35 0.06 0.29 动摩擦因数 0.26 0.32 1.2 0.59 静摩擦因数 0.34 0.47 1.13 0.48 
下载: 导出CSV
表 2 试验变量编码水平表
Table 2 Experimental variable encoding level table
编码值
Coded value排肥器开度
Opening L/mm排肥器转速
Speed N/(r·min−1)−1 20 20 1 45 60
下载: 导出CSV
表 3 模型训练的R2和MAPE
Table 3 R2 and mean absolute percentage error obtained from model training
训练次数
Number of training iterationsMLP PSO-MLP LFA-PSO-MLP R2 MAPE R2 MAPE R2 MAPE 1 0.943 13.01 0.992 2.87 0.998 1.93 2 0.993 2.79 0.999 1.80 3 0.989 2.99 0.998 1.83 4 0.995 2.80 0.998 1.89 5 0.987 3.08 0.999 1.77 6 0.989 3.02 0.999 1.80 7 0.991 2.94 0.998 1.84 8 0.988 2.99 0.998 1.84 9 0.99 2.96 0.999 1.79 10 0.992 2.92 0.998 1.84 均值 0.988 2.95 0.999 1.83 稳定拟合代数 300 / 50
下载: 导出CSV
表 4 排肥量验证值与预测值的对比
Table 4 Comparison between validation and predicted values of fertilizer application amounts
序号
No.开度 Opening L/
mm转速 Speed N/
(r·min−1)验证值
Verification value Q/
(g·min−1)预测值
Predicted value P/(g·min−1)相对误差
Relative
error/%1 23 23 1020.438 1034.406 1.37 2 23 33 1390.638 1419.156 2.05 3 23 43 1751.322 1821.186 3.99 4 23 53 2151.618 2213.298 2.87 5 23 63 2504.772 2595.048 3.6 6 35 23 1435.152 1428.222 0.48 7 35 33 2044.548 2003.796 1.99 8 35 43 2627.13 2559.702 2.57 9 35 53 3212.91 3156.564 1.75 10 35 63 3829.41 3721.314 2.82 11 43 23 1866.858 1824.606 2.26 12 43 33 2642.034 2556.012 3.26 13 43 43 3415.578 3322.296 2.73 14 43 53 4182.63 4065.072 2.81 15 43 63 4911.174 4791.09 2.45
下载: 导出CSV
表 5 ILMP模型预测结果
Table 5 Result related to inverse prediction of the ILMP model
序号
No.目标排肥量
Verification value Q/
(g·min−1)开度
Opening L /mm转速参考值
Reference value N/
(r·min−1)转速预测值
Predicted value Np/
(r·min−1)相对误差
Relative error /%1 1020.438 23 23 23.53 2.30 2 1390.638 23 33 32.48 1.58 3 1751.322 23 43 43.96 2.23 4 2151.618 23 53 54.01 1.91 5 2627.13 35 43 42.39 1.42 6 3212.91 35 53 53.64 1.21 7 3829.41 35 63 64.59 2.52 8 4182.63 43 53 54.12 2.11 9 4911.174 43 63 62.33 1.06
下载: 导出CSV
表 6 排肥量的实测值和预测值及其相关数据
Table 6 Measured and predicted values of fertilizer distribution and their correlation data
试验序号
No.开度
Opening转速组合
Speed combination排肥量实测值
Measured value /(g·min−1)排肥量预测值
Predicted value /(g·min−1)相对误差
Relative error/%1 25 30 1388.74 1466.27 5.59 2 25 40 1822.21 1886.69 3.54 3 25 50 2330.98 2276.31 2.35 4 30 30 1649.75 1580.16 4.22 5 30 40 2207.43 2101.32 4.81 6 30 50 2431.96 2531.3 4.08 7 40 30 2269.11 2173.96 4.19 8 40 40 2897.16 2926.71 1.02 9 45 40 3347.4 3210.62 4.09 10 45 50 4137.22 4094.76 1.03
下载: 导出CSV
表 7 搭载ILMP模型的施肥机排肥结果
Table 7 Fertilization results of the fertilizer applicator equipped with the ILMP model
试验序号
Test No.目标排肥量
Target value/g实际排肥量
Measured value /g单位时间排肥量
Measured value per time/(g·min−1)相对误差
Relative error /%1 5612.93 5260.72 3507.15 6.70 2 5960.31 5605.16 3803.44 6.34 3 5821.91 5428.03 3752.02 7.26 4 5647.63 5293.44 3528.96 6.69 5 6064.18 5655.98 3770.65 7.22 6 5777.36 5645.73 3763.82 2.33
下载: 导出CSV
-
[1] 施印炎. 基于水稻光谱信息的离心式变量撒肥机的研制[D]. 南京:南京农业大学,2018. SHI Yinyan. Design on Variable Fertilizer Spreader with Centrifugal Discs in Spectral Reflectance for Rice Field [D]. Nanjing: Nanjing Agricultural University, 2018. (in Chinese with English abstract)
[2] 任灵杰,田敏,李江全,等,我国变量施肥技术的研究现状与发展分析[J]. 农机化研究,2023,45(10):10-15,23. REN Lingjie, TIAN Min, LI Jiangquan, et al. Research status and development analysis of variable fertilization technology in China[J]. Journal of Agricultural Mechanization Research, 2023, 45(10): 10-15, 23. (in Chinese with English abstract)
[3] 陈金,赵斌,衣淑娟,等. 我国变量施肥技术研究现状与发展对策[J]. 农机化研究,2017,39(10):1-6. CHEN Jin, ZHAO Bin, YI Shujuan, et al. Research on present situation and the development countermeasures of variable rate fertilization technology in China[J]. Journal of Agricultural Mechanization Research, 2017, 39(10): 1-6. (in Chinese with English abstract)
[4] 施印炎,陈满,汪小旵,等. 离心匀肥罩式水稻地表变量撒肥机设计与试验[J]. 农业机械学报,2018,49(3):86-93, 113. SHI Yinyan, CHEN Man, WANG Xiaofan, et al. Design and experiment of variable-rate fertilizer spreader with centrifugal distribution cover for rice paddy surface fertilization[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(3): 86-93, 113. (in Chinese with English abstract)
[5] 梁宇超,汤智辉,纪超,等. 外槽轮排肥器结构参数优化与试验[J]. 农机化研究,2023,45(12):7-14. DOI: 10.3969/j.issn.1003-188X.2023.12.002 LIANG Yuchao, TANG Zhihui, JI Chao, et al. Optimization and experiment of structural parameters of outer groove wheel fertilizer drainer[J]. Journal of Agricultural Mechanization Research, 2023, 45(12): 7-14. (in Chinese with English abstract) DOI: 10.3969/j.issn.1003-188X.2023.12.002
[6] 顿国强,刘文辉,杜佳兴,等. 弧槽双螺旋式排肥器优化设计与试验[J]. 农业机械学报,2022,53(10):118-125, 174. DUN Guoqiang, LIU Wenhui, DU Jiaxing, et al. Optimal design and experiment of arc-groove double-spiral fertilizer discharge device[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(10): 118-125, 174. (in Chinese with English abstract)
[7] 陈满,施印炎,汪小旵,等. 基于光谱探测的小麦精准追肥机设计与试验[J]. 农业机械学报,2015,46(5):26-32. CHEN Man, SHI Yinyan, WANG Xiaofan, et al. Design and experiment of variable rate fertilizer applicator based on crop canopy spectral reflectance[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 26-32. (in Chinese with English abstract)
[8] YUAN J, LIU C, LI Y, et al. Gaussian processes based bivariate control parameters optimization of variable-rate granular fertilizer applicator[J]. Computers and Electronics in Agriculture, 2009, 70(1): 33-41.
[9] 李井竹,刘秋菊,王仲英. 基于改进SSA算法优化极限学习机模型的土壤供肥量预测[J]. 中国农机化学报,2023,44(10):174-184. LI Jingzhu, LIU Qiuju, WANG Zhongying. Prediction of soil fertilizer for optimizing extreme learning machine based on improved SSA algorithm[J]. Journal of Chinese Agricultural Mechanization, 2023, 44(10): 174-184. (in Chinese with English abstract)
[10] 郑宏艳,刘书田,侯彦林,等. 生态平衡施肥模型与肥料效应函数模型关系研究[J]. 农业资源与环境学报,2014,31(6):500-505. ZHENG Hongyan, LIU Shutian, HOU Yanlin, et al. Relationship of ecological balanced fertilization model and fertilizer effect function method[J]. Journal of Agricultural Resources and Environment, 2014, 31(6): 500-505. (in Chinese with English abstract)
[11] 何修君. 基于机器学习的玉米产量预测模型研究[D]. 长春:吉林农业大学,2021. HE Xiujun. Research on Maize Yield Prediction Model Based on Machine Learning [D]. Changchun: Jilin Agricultural University, 2021. (in Chinese with English abstract)
[12] 王学智. 基于深度学习的土壤温湿度预测相关技术研究[D]. 长春:吉林大学,2022. WANG Xuezhi. Research on Related Technologies of Soil Temperature and Soil Moisture Prediction Based on Deep Learning [D].Changchun: Jilin University, 2022. (in Chinese with English abstract)
[13] 安树杰. 应用遥感与GIS的松材线虫病预测模型的研究[D]. 北京:北京林业大学,2006. AN Shujie. The Research on Predictive Model of Bursaphelenchus Xylophilus by RS and GIS [D]. Beijing: Beijing Forestry University, 2006. (in Chinese with English abstract)
[14] 贾海峰,李玥峤,黄帅,等. 基于云计算与RBF神经网络集成的玉米精准施肥模型研究[J]. 玉米科学,2023,31(6):128-134. JIA Haifeng, LI Yueqiao, HUANG Shuai, et al. Research on accurate fertilization model of maize based on cloud computing and RBF neural network[J]. Journal of Maize Sciences, 2023, 31(6): 128-134. (in Chinese with English abstract)
[15] 杨烁楠,李玉成,史杨,等.土壤有机质空间分布预测与草莓种植分区施肥方案——以长丰县为例[J].农业资源与环境学报,2024,41(03):585-591. 4-02-08]. YANG Shuonan, LI Yucheng, SHI Yang, et al. Prediction of spatial distribution of soil organic matter and fertilization plan for strawberry planting zones - a case study of changfeng county [J]. Journal of Agricultural Resources and Environment, 2024,41(03):585-591. (in Chinese with English abstract)
[16] 黄珍,刘涛. 基于神经网络算法的精准施肥模型建立及仿真分析[J]. 现代农业研究,2023,29(11):45-50. DOI: 10.3969/j.issn.1674-0653.2023.11.010 HUANG Zhen, LIU Tao. Establishment and simulation analysis of precision fertilization model based on neural network algorithm[J]. Modern Agricultural Research, 2023, 29(11): 45-50. (in Chinese with English abstract) DOI: 10.3969/j.issn.1674-0653.2023.11.010
[17] 张季琴,刘刚,仁重义,等. 基于GWO-GRNN的双变量施肥系统排肥量预测模型构建[J]. 江苏农业科学,2023,51(2):210-217. ZHANG Jiqin, LIU Gang, REN Zhongyi, et al. Construction of fertilizer rate prediction model for bivariate fertilization system based on GWO-GRNN[J]. Jiangsu Agricultural Sciences, 2023, 51(2): 210-217. (in Chinese with English abstract)
[18] 张季琴,刘刚,张东峰,等. 固体颗粒肥变量撒施控制技术研究现状与展望[J]. 江苏农业科学,2022,50(20):69-77. ZHANG Jiqin, LIU Gang, ZHANG Dongfeng, et al. Research status and prospect on granular fertilizer variable-rate control technology[J]. Jiangsu Agricultural Sciences, 2022, 50(20): 69-77. (in Chinese with English abstract)
[19] 巩海亮. 基于NDVI的玉米中耕变量施肥实时预测调控系统研究[D].大庆:黑龙江八一农垦大学,2021. GONG Hailiang. Research on the Real-time Predictive Control System of Variable Fertilization in Corn Field Cultivation Based on NDVI [D]. Daqing: Heilongjiang Bayi Agricultural University, 2021. (in Chinese with English abstract)
[20] 施印炎,陈满,汪小旵,等. 稻麦精准追肥机执行机构的设计与试验[J]. 华南农业大学学报,2015,36(6):119-124. SHI Yinyan, CHEN Man, WANG Xiaofan, et al. Design and experiment of precision fertilizer applicator actuator of rice and wheat[J]. Journal of South China Agricultural University, 2015, 36(6): 119-124. (in Chinese with English abstract)
[21] 施印炎,陈满,汪小旵,等. 稻麦精准变量施肥机排肥性能分析与试验[J]. 农业机械学报,2017,48(7):97-103. SHI Yinyan, CHEN Man, WANG Xiaofan, et al. Analysis and experiment of fertilizing performance for precision fertilizer applicator in rice and wheat fields[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(7): 97-103. (in Chinese with English abstract)
[22] 冯茜,李擎,全威,等. 多目标粒子群优化算法研究综述[J]. 工程科学学报,2021,43(6):745-753. FENG Xi, LI Qing, QUAN Wei, et al. Overview of multiobjective particle swarm optimization algorithm[J]. Chinese Journal of Engineering, 2021, 43(6): 745-753. (in Chinese with English abstract)
[23] 马学森,谈杰,陈树友,等. 云计算多目标任务调度的优化粒子群算法研究[J]. 电子测量与仪器学报,2020,34(8):133-143. MA Xuesen, TAN Jie, CHEN Shuyou, et al. Research on optimal particle swarm optimization for multi-objective task scheduling in cloud computing[J]. Journal of Electronic Measurement and Instrumentation, 2020, 34(8): 133-143. (in Chinese with English abstract)
[24] 兰少峰,刘升. 布谷鸟搜索算法研究综述[J]. 计算机工程与设计,2015,36(4):1063-1067. LAN Shaofeng, LIU Sheng. Overview of research on cuckoo search algorithm[J]. Computer Engineering and Design, 2015, 36(4): 1063-1067. (in Chinese with English abstract)
[25] 王庆喜,郭晓波. 基于莱维飞行的粒子群优化算法[J]. 计算机应用研究,2016,33(9):2588-2591. WANG Qingxi, GUO Xiaobo. Particle swarm optimization algorithm based on levy flight[J]. Application Research of Computers, 2016, 33(9): 2588-2591. (in Chinese with English abstract)
[26] 张驰,郭媛,黎明. 人工神经网络模型发展及应用综述[J]. 计算机工程与应用,2021,57(11):57-69. ZHANG Chi, GUO Yuan, LI Ming. Review of development and application of artificial neural network models[J]. Computer Engineering and Applications, 2021, 57(11): 57-69. (in Chinese with English abstract)
[27] 晏福,徐建中,李奉书. 混沌灰狼优化算法训练多层感知器[J]. 电子与信息学报,2019,41(4):872-879. YAN Fu, XU Jianzhong, LI Fengshu. Training multi-layer perceptrons using chaos grey wolf optimizer[J]. Journal of Electronics & Information Technology, 2019, 41(4): 872-879. (in Chinese with English abstract)
[28] AHAKONYE C A L , ZAINUDIN A , SHANTO A J M , et al. A multi-MLP prediction for inventory management in manufacturing execution system[J]. Internet of Things, 2024, 26.
[29] VAGHEFI E HOSSEINI S , PROROK B , et al. Geometrically-informed predictive modeling of melt pool depth in laser powder bed fusion using deep MLP-CNN and metadata integration[J]. Journal of Manufacturing Processes, 2024, 119952-963.
[30] 郭丽峰. 立式圆盘大豆排种器型孔优化设计与试验研究[D]. 哈尔滨:东北农业大学,2014. GUO Lifeng. Optimal Design and Experimental Research on the Type Hole of Vertical Disk Soybean Seed Metering Device [D]. Harbin: Northeast Agricultural University, 2014. (in Chinese with English abstract)
[31] SHI Y Y, CHEN M, WANG X C, et al. Efficiency analysis and evaluation of centrifugal variable-rate fertilizer spreading based on real-time spectral information on rice[J]. Computers and Electronics in Agriculture, 2023, 204: 107505. DOI: 10.1016/j.compag.2022.107505
计量
- 文章访问数: 1
- HTML全文浏览量: 2
- PDF下载量: 0
下载:
