高级检索+

基于SHAP重要性排序和机器学习算法的灌区渠道调度流量预测

葛建坤, 雷国相, 陈皓锐, 张宝忠, 陈来宝, 白美健, 苏楠, 于子慧

葛建坤，雷国相，陈皓锐，等. 基于SHAP重要性排序和机器学习算法的灌区渠道调度流量预测[J]. 农业工程学报，2023，39（13）：113-122. DOI: 10.11975/j.issn.1002-6819.202304081
引用本文: 葛建坤，雷国相，陈皓锐，等. 基于SHAP重要性排序和机器学习算法的灌区渠道调度流量预测[J]. 农业工程学报，2023，39（13）：113-122. DOI: 10.11975/j.issn.1002-6819.202304081
shu
GE Jiankun, LEI Guoxiang, CHEN Haorui, et al. Irrigation district channel dispatch flow prediction based on SHAP importance ranking and machine learning algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(13): 113-122. DOI: 10.11975/j.issn.1002-6819.202304081
Citation: GE Jiankun, LEI Guoxiang, CHEN Haorui, et al. Irrigation district channel dispatch flow prediction based on SHAP importance ranking and machine learning algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(13): 113-122. DOI: 10.11975/j.issn.1002-6819.202304081
shu

基于SHAP重要性排序和机器学习算法的灌区渠道调度流量预测

  • 1.

    华北水利水电大学水利学院，郑州 450045

  • 2.

    中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京100048

  • 3.

    国家节水灌溉北京工程技术研究中心，北京 100048

  • 4.

    安徽省淠史杭灌区管理总局，六安 237005

基金项目: 十四五国家重点研发计划课题（2022YFD1900504）；中国水利水电科学研究院技术创新团队项目（ID145B022021）；河南省高等学校青年骨干教师培养计划项目（2020GGJS100）
详细信息
    作者简介:

    葛建坤，博士，副教授，研究方向为农业水资源高效利用。Email：54012012@qq.com

    通讯作者:

    陈皓锐，正高级工程师，研究方向为灌区水循环模拟与调控。Email: chenhr@iwhr.com

  • 中图分类号: TV122

Irrigation district channel dispatch flow prediction based on SHAP importance ranking and machine learning algorithm

  • 1.

    College of Water Resources of North China University of Water Conservancy and Hydropower, Zhengzhou 450045, China

  • 2.

    State Key Laboratory of Basin Water Cycle Simulation and Regulation, China Institute of Water Resources and Hydropower Research, Beijing 100048, China

  • 3.

    National Water Conservation Irrigation Engineering Technology Research Center, Beijing 100048, China

  • 4.

    Anhui Province General Administration of Irrigation District, Liu'an 237005, China

摘要

    摘要
  • 摘要:

    渠道泄水闸能够快速排除灌区入渠洪水，避免渠道漫顶。研究以淠史杭灌区灌口集泄水闸为例，以闸门调度流量为目标变量，以不同时段过去和未来降雨量、泄水闸闸上实时水位及其变化量为特征变量，比较8种机器学习算法的预测精度，同时采用shapley additive explanations（SHAP）法分析特征变量重要性。结果表明：1）集成学习算法预测评价指标优于传统回归算法，8种机器学习算法中随机森林回归（random forest regression, RFR）算法预测精度最高（训练集均方根误差、平均绝对误差、均方误差及决定系数分别为 0.146 m3/s、0.094 m3/s、0.021 m3/s、0.976；测试集分别为0.306 m3/s、0.197 m3/s、0.093 m3/s、0.931）；2）采用SHAP法确定的特征变量重要性排序表明灌口集泄水闸闸上水位对于泄水闸调度流量的预测结果影响最大，占特征重要性值总和的34.6%；3）以过去6 h降雨量、过去9 h降雨量、未来6 h降雨量、灌口集泄水闸闸上水位作为输入变量的RFR算法预测灌口集泄水闸调度流量效果最佳，训练集均方根误差、平均绝对误差、均方误差及决定系数分别为0.126 m3/s、0.080 m3/s、0.016 m3/s、0.982；测试集分别为0.263 m3/s、0.164 m3/s、0.069 m3/s、0.950，研究结果对灌区防洪调度决策具有重要参考价值。

    Abstract:

    The channel sluice can quickly remove the flood into the canal in the irrigation area. In order to provide a simple and efficient method for flood control scheduling decision of drainage sluice in irrigation area, this study took Pishihang Irrigation District as an example to establish a prediction model with dispatched flow as the target variable and 10 characteristic variables as independent variables. The 10 variables were the water level and rainfall of drainage sluice at irrigation mouth: rainfall in the past 1 hour, 2 hour, 3 hour, 6 hour, and 9 hour and rainfall in the future 1 hour, 3 hour and 6 hour, water level on the gates of the Guan Kouji drainage gate, difference in water level at the gate in the past half hour.The prediction accuracy of 8 machine learning algorithms was compared to pick the best algorithm. The Shapley Additive exPlanations（SHAP）method was used to analyze the importance of 10 groups of variables, and the influence weights of different variables on the prediction results were obtained. By comparing the prediction error indicators of the optimal algorithm under different variable combinations, the optimal variable combinations were selected, and the accuracy of the algorithm was further optimized to determine the final scheduling flow decision model. The results showed that: 1) The integrated learning algorithm was better than the traditional regression algorithm in predicting the evaluation index. The order of prediction accuracy of ensemble learning algorithms was as follows: random forest regression （RFR）>extrme gradient boosting regression (XGR) >adapative bossting regression (ABR)>spoort vector regression (SVR), and Bagging had the highest accuracy in the three categories of ensemble learning algorithms. RFR had the highest prediction accuracy among the 8 machine learning algorithms (the root mean square error, mean absolute error, mean square error and determination coefficient of the training set were 0.146, 0.094, 0.021 m3/s and 0.976, respectively. The root-mean-square error, mean absolute error and mean square error of the test set were 0.306, 0.197, 0.093 m3/s and 0.931, respectively); 2) The importance values of characteristic variables determined by SHAP method were as follows in descending order: water level on the gates of the Guan Kouji drainage gate, rainfall in the past 9 hour, rainfall in the future 6 hour, rainfall in the past 6 hour, rainfall in the past 3 hour, rainfall in the past 2 hour, rainfall in the future 1 hour, rainfall in the past 1 hour, difference in water level at the gate in the past half hour and rainfall in the future 3 hour. The water level on the gates of the Guan Kouji drainage gate had the greatest influence on the prediction results of the drainage flow, accounting for 34.6% of the total importance values of the features. The total importance values of the rainfall features in the past period were 0.473, and the total importance values of the rainfall features in the future period were 0.287. The influence degree of the rainfall in the past period was greater than that of the rainfall in the future. 3) The RFR algorithm with the input variables of past 6 hour rainfall, past 9 hour rainfall, future 6 hour rainfall and the water level on the gates of the Guan Kouji drainage gate was the best to predict the dispatching flow of the sluice gate (The model error indexes were as follows: root mean square error, mean absolute error, mean square error and determination coefficient of training set are 0.126, 0.080, 0.016 m3/s and 0.982, respectively; The root mean square error, mean absolute error, mean square error and determination coefficient of the test set were 0.263, 0.164, 0.069 m3/s and 0.950, respectively. The determination coefficients of the training set and the test set were increased by 0.6% and 2.0%, respectively, compared with all the characteristic variables. The root-mean-square error, mean absolute error and mean square error were reduced by 13.7%, 14.9%, 23.8%, 14.1%, 16.3% and 25.8%, respectively, compared with all the characteristic variables. It can be seen that variable selection has a significant impact on the prediction accuracy. This study avoids the multi-source data collection and complex operation required by the coupling mechanism model, and provides technical support for the irrigation district management agency to scientifically dispatch the sluice of each channel. The research results were of great significance for realizing the modernization of irrigation district.

    • HTML全文

  • 0.   引　言

    灌区渠道除接受上游水库/渠道的供水外，还可能接受沿程的坡面汇流、平交河道的洪水汇入，在暴雨条件下，渠道上游来流叠加沿程的各种面状（坡面洪水）和线状汇流（平交河道汇流），可能会导致渠道水位过高，影响渠道的安全运行，灌区泄水闸能够快速宣泄这部分洪水，确保汛期渠道安全。因此，如何合理的进行渠道泄水闸的决策是灌区管理者在汛期需要面对的问题。与自然流域洪水过程类似，渠道洪水的发生和推进也包括渠道沿程集水区的降雨产汇流过程和洪水在渠道中的演进过程；与其不同的是，渠道中节制闸、分水闸和泄水闸的人工调度会对洪水入渠后的推进过程有较大的影响，其边界条件较自然流域更为复杂，这也给合理开展渠道防洪调度带来了挑战。

    基于物理机制的明渠/河道泄水需在摸清灌区渠道来水汇入点、沿程汇流集水区、泄水点和分水点的空间分布和水力拓扑关系的基础上，通过耦合产汇流模型、一维明渠水流运动和调度优化模型进行防洪调度决策优化。防洪调度是一个非线性复杂决策过程，这使得调度方案的优化决策难以实现[1-2]。基于物理机制的防洪调度优化方法主要分为线性规划（linear programming, LP）、非线性规划（non-linear programming, NLP）、动态规划（dynamic programming, DP）、鹈鹕优化算法（pelican optimization algorithm, POA）和遗传算法等。李其梁等[3]建立了基于线性规划的两湖河道联合调度数学模型，可为汛期洪水资源配置提供决策依据。非线性规划能够处理目标函数不可分和非线性约束问题，能够应用于更复杂的优化调度场景中，林瑜等[4]构建了基于马斯京根模型的非线性规划模拟河段渠道中的洪水演进过程，为汛期渠道断面流量决策提供了可靠的方法。但LP和NLP方法不能考虑单个泄水闸的状态，因此不适合处理灌区渠道调度决策问题。ZHAO等[5]将单调关系与动态规划进行合并，提出了改进DP 的新算法，该算法可以作为防洪调度的有用工具测试不同的洪水情景并确定最优决策。LIU等[6]利用POA方法确定了考虑河道优化的汛期多目标最优调度规则。但DP和POA计算工作量大，泄水闸数量较多时，容易造成“维数灾难”，需要一定的降维方法。AFAN等[7]以尼罗河高阿斯旺大坝为研究对象，采用遗传算法优化了河流流量的预测精度，确定了时间序列下预测洪水的有效输入参数，研究结果可为其他类似地区的河道防洪调控提供参考。但遗传算法编程较为复杂，且算法内包含的交叉率、变异率等参数的设定依然需要人工经验确定。基于物理机制的防洪调度优化模型不仅在各环节的物理过程控制方程的求解和耦合方面较为复杂，而且涉及大量的模型参数，其实际应用过程中对数据资料的要求和模型使用者的专业要求较高。因此，如果能够基于影响渠道泄水决策的主要影响因素获得相对容易监测的数据，开展渠道防洪调度的决策，可以避免上述物理机制模型的缺点。

    近年来，人工智能技术发展迅速，机器学习作为人工智能技术的核心分支，能够学习经验数据中输入和输出之间的复杂关系，快速提取高维数据特征和处理非线性数据，且具有良好的容错性[8]。高玮志等[9]利用机器学习解决了太湖流域多层次防洪调度方案的评价问题。张帆等[10]采用多种机器学习模型对洪水特征指标进行了评估，为防洪措施的制定提供了参考。尽管机器学习算法在先前研究中表现良好，但由于其特有的“黑箱”性质，无法解释各变量对预测结果的贡献程度。Shapley Additive exPlanations（SHAP）作为当前热门的机器学习事后解释工具，能够检测特征之间的交互作用，从而提供更加全面的特征重要性排序结果[11-12]。目前已用于环境监测、土地利用、信息科学等[11,13-14]重要领域，该方法能够清楚量化机器学习算法中特征变量的全局重要性，可为防洪调度中关键因素的识别以及机器学习算法优化提供重要帮助。

    目前，灌区渠道防洪调度决策依赖复杂物理机制的调度优化模型，决策者需要对各渠段在不同暴雨条件下的来洪过程、洪量和洪峰大小、渠道的承洪能力、泄洪效果等非常了解才能做出较为合理的调度决策，若了解不充分，则可能造成渠道水量过度下泄等问题，危害下游渠系建筑物的安全。鉴于此，为给灌区渠道防洪调度决策提供一种简单高效的方法，本研究以安徽淠史杭灌区灌口集泄水闸为例，基于实测的闸上水位、历史和预报降雨信息以及泄水调度流量数据，比较不同机器学习算法的预测精度，同时采用SHAP法筛选特征变量组合，进一步优化算法精度。以期为灌区现代化管理提供技术支撑。

    1.   材料与方法

    1.1   研究区概况

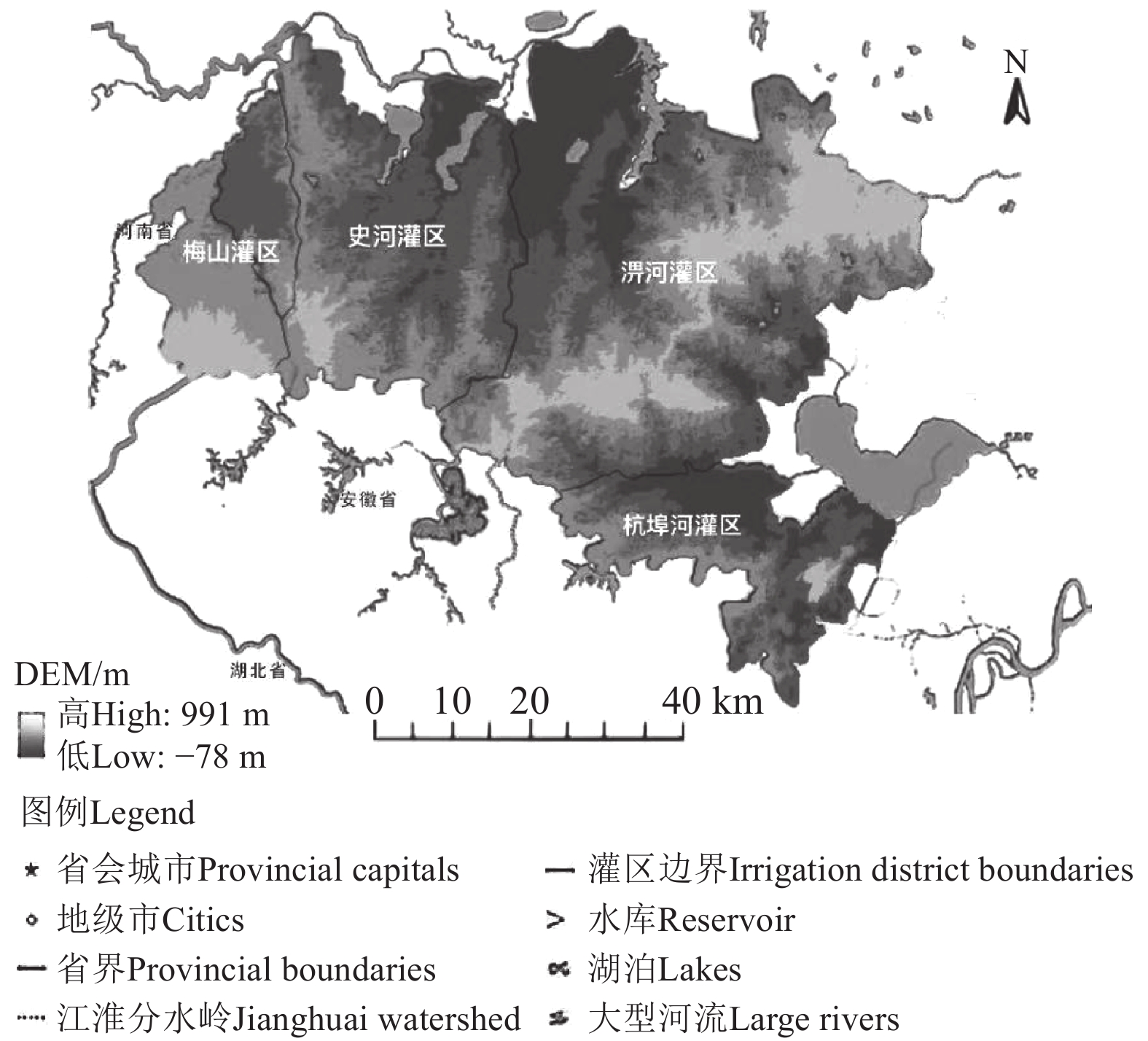
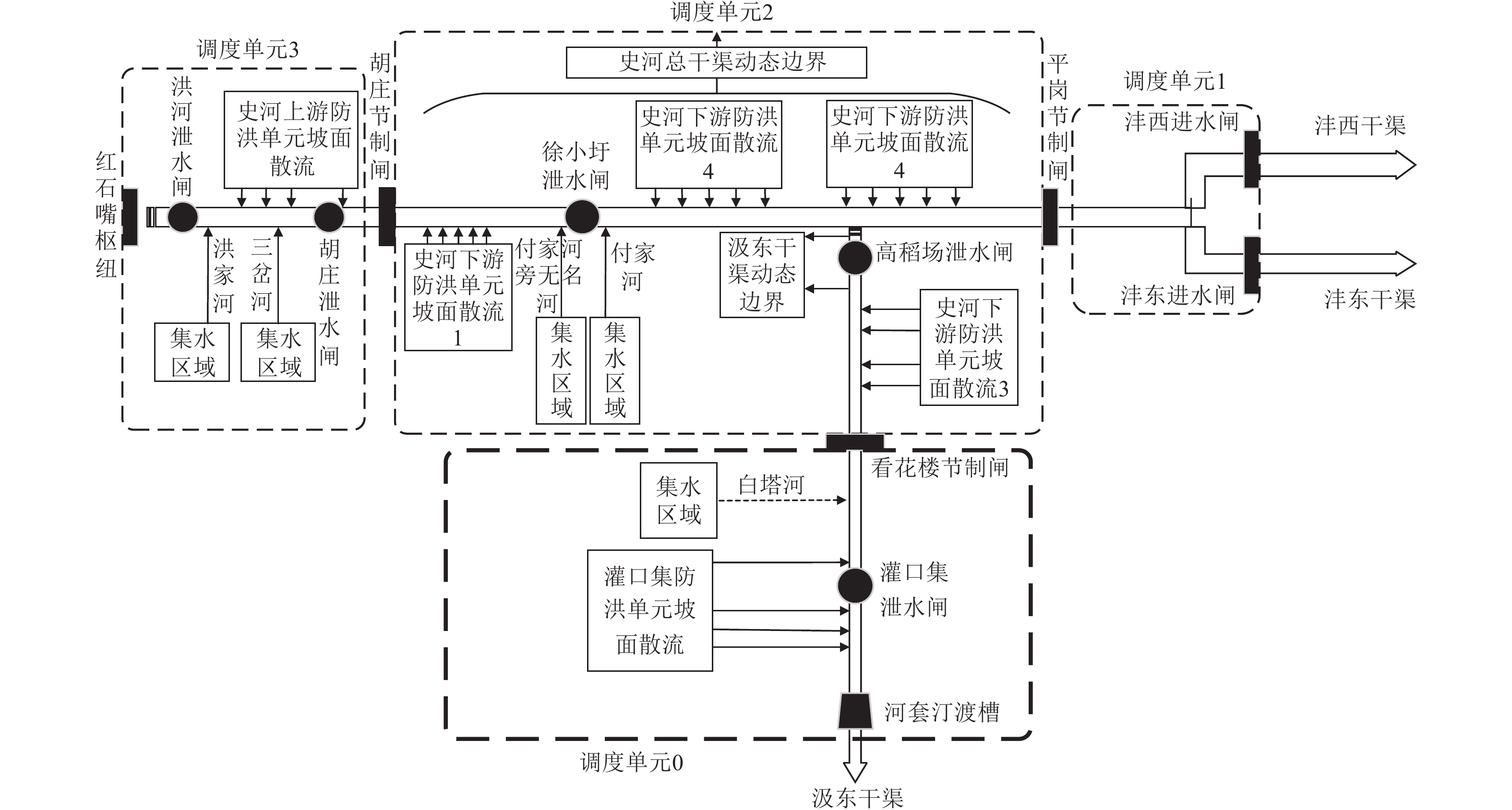
    淠史杭灌区位于安徽省中西部和河南省东南部，是中国特大灌区之一。其中安徽部分由淠河、史河、杭埠河三大灌区组成（图1）。灌区地貌包括山丘和平原两大类型，对于途经山丘区的渠段，在遭遇暴雨时，渠道一侧坡面的降雨产流会汇入渠道，引起渠道水位过高，从而引发渠道运行安全问题，该问题在南方丘陵灌区具有典型代表性。史河灌区位于淠史杭灌区西部，该灌区的局管渠道包括5个泄水闸，渠道防汛调度以节制闸为界划分为4个调度单元，各调度单元来洪基本在单元内排除。灌口集调度单元进口为看花楼节制闸，出口为河套汀渡槽，该单元有2片侧向坡面来水，分别通过白嗒河和坡面散流进入渠道，单元内设置了灌口集泄水闸用于排除洪水。灌口集泄水闸单孔闸宽7 m，共5孔，设计流量265 m3/s，闸上设计水位57.32 m。

    图  1  淠史杭灌区示意图
    注：DEM为地表高程。
    Figure  1.  Schematic diagram of irrigation area of Pi Shihang
    Note: DEM is the surface elevation.
    下载: 全尺寸图片 幻灯片

    1.2   影响因素分析和数据来源

    灌区渠道泄洪调度期间，对于特定的泄水闸而言，其所在渠道的集水区面积、土壤质地、下垫面条件、集水区坡面/入渠河道的地形和坡度、坡面或者入渠河道的糙率、渠道断面和坡度、渠道糙率等因素一般固定不变。灌区渠道在汛期关闭进水闸或分水闸时，渠道无上游来水，洪水完全来自单元流域内的降雨[15]。渠道水位是汛期灌区管理人员进行洪水调度时的首要关注指标，各泄水闸段的渠道水位不能超过警戒水位，防止漫顶[16]。通过咨询灌区管理部门可知，对于灌口集调度单元而言，当启动防洪调度时，单元进口闸（看花楼节制闸）关闭，即渠道上游来流始终为0，该单元沿渠也未受其他闸门影响（图2）。因此，灌口集泄水闸的调度方式主要取决于过去的落地雨量、未来预报的雨量以及泄水闸前的实时水位及动态变化量。为尽可能全面考虑泄水闸调度的影响因素，本研究选取过去1、2、3、6、9 h和未来1、3、6 h累积降雨量、灌口集泄水闸闸上水位和闸上水位差作为特征变量，以灌口集泄水闸调度流量作为目标变量（表1），其中降雨量以集水片区内部及其附近的8个降雨站点平均值代表面雨量（白塔畈、龚店、薛贩、万山桥、小高庙、朱小堰、红石嘴、梅山）。上述各类数据来源于安徽省水文局和淠史杭灌区管理总局。

    图  2  灌口集泄水单元连接关系图
    Figure  2.  Guan Kouji drainage unit connection relationship diagram
    下载: 全尺寸图片 幻灯片
    表  1  变量及说明
    Table  1.  Variables and descriptions
    符号
    Symbols    		说明
    Description    		单位
    Units    		数据系列长度
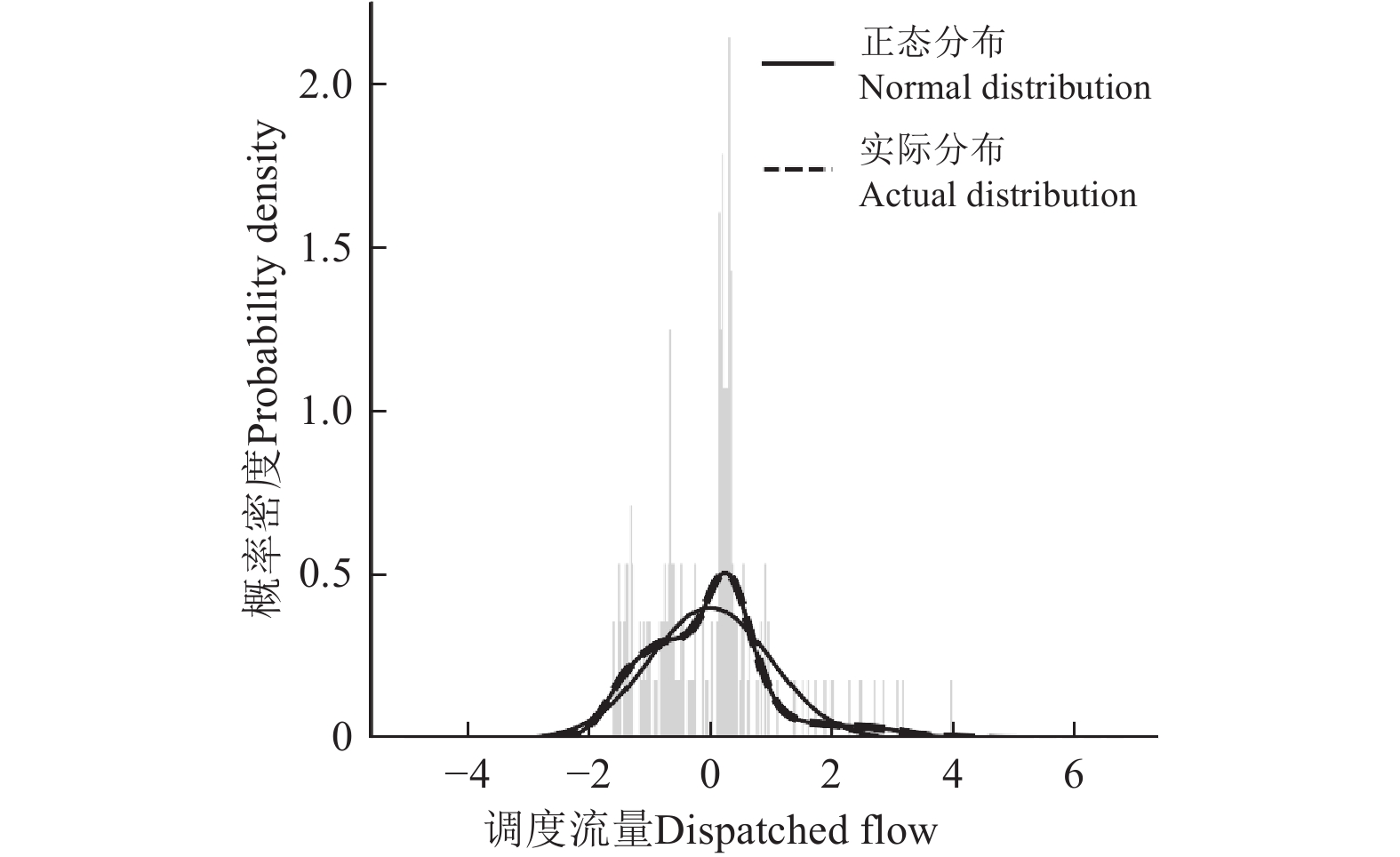
    Data series length
    x1过去1 h降雨量mm2010—2020年
    x2过去2 h降雨量mm
    x3过去3 h降雨量mm
    x4过去6 h降雨量mm
    x5过去9 h降雨量mm
    x6未来1 h降雨量mm
    x7未来3 h降雨量mm
    x8未来6 h降雨量mm
    x9灌口集泄水闸闸上水位m
    x10过去0.5 h闸上水位差m
    Y灌口集泄水闸调度流量m3·s−1
    下载: 导出CSV 
    | 显示表格

    为检验特征变量是否能解释调度流量变化规律，对灌口集泄水闸调度流量Y进行分析。由图3可以看出，调度流量分布曲线在偏度及峰度上与正态分布曲线均有一定的相似度，采用柯尔莫哥洛夫-斯米尔诺夫检验（kolmogorov-smirnov, K-S检验）得到变量Y及x1～x10的P值分别为0.225、0.140、0.131、0.133、0.121、0.075、0.130、0.122、0.135、0.232、0.208（P>0.05），均服从正态分布，参考文献[17]，将x1～x10全部用于算法预测及验证。

    图  3  灌口集泄水闸调度流量分布曲线
    Figure  3.  Distribution curve of dispatching flow of Guan Kouji drainage gate
    下载: 全尺寸图片 幻灯片

    1.3   研究方法

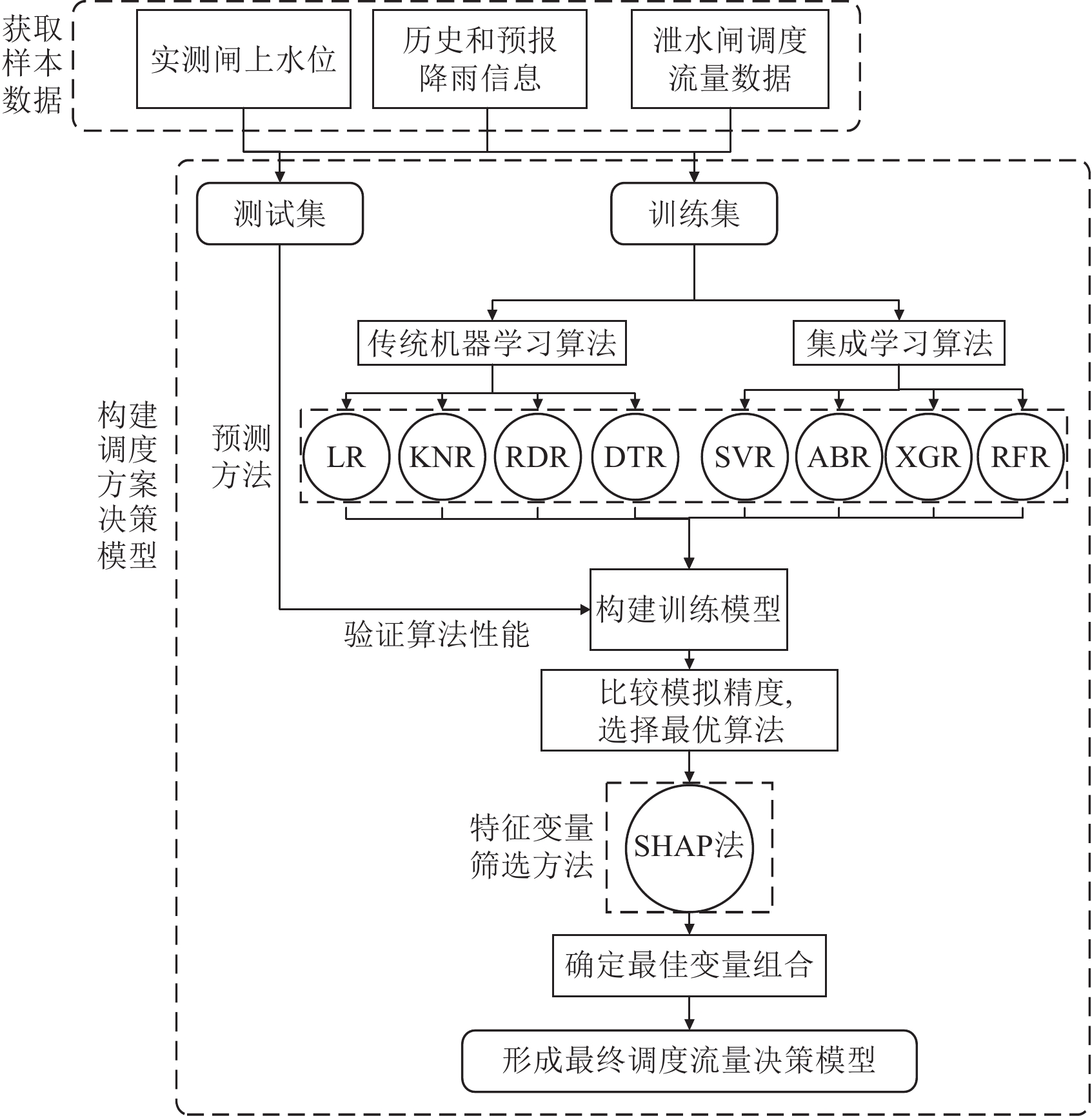
    本研究所用方法分为预测方法和特征变量筛选方法两大类，其中预测方法用来建立特征变量与调度流量之间的关系，特征变量筛选方法是在分析特征变量对调度流量预测结果的影响程度大小的基础上，筛选变量组合。预测方法选取了线性回归（linear regression, LR）、K近邻回归（k-nearest neighbors regressor, KNR）、岭回归（ridge regression, RDR）、决策树回归（decision tree regression, DTR）4种传统回归算法和支持向量回归（support vector regression, SVR）、自适应提升回归（adaptive boosting regression, ABR）、极度梯度提升回归（extreme gradient boosting, regression, XGR）、随机森林回归（random forest regression, RFR）4种集成学习算法进行比较。传统回归算法中LR可判断变量与目标因子之间线性相关程度的强弱[18]。KNR适宜对连续时间的数据进行预测[19]，符合本研究的数据类型。RDR能够处理自变量间多重共线性问题[20]。DTR能够表现数据间复杂的非线性关系，对缺失值不敏感且训练速度较快，适合用于小规模数据集的回归预测[21]。集成学习算法能够串联传统机器学习算法中的多个基学习器，提高预测性能。本文采用的4种集成学习算法可分为3类，其中SVR和RFR分别属于堆叠算法（stacking）和装袋算法（bagging），ABR和XGR属于提升算法（boosting）。Stacking集成的高层模型使用线性回归等基学习器进行组合输出[22]，bagging使用同质弱学习器，其输出投票或平均产生，最终获得比基学习器更小的方差；boosting串联各个基学习器调整样本的损失函数或权重，通过叠加来减少总模型的预测偏差[23]。其中ABR和XGR在拟合残差方式上有所不同。8种机器学习算法的关键参数及说明见表2。

    表  2  算法参数及说明
    Table  2.  Algorithm parameters and description
    分类 Type算法 Algorithm参数及解释 Parameter and its explanation取值 Value
    传统回归算法
    Traditionl regression algorithm    		线性回归（LR）是否需要计算截距fit_interceptTrue
    是否复制训练数据copy_XTrue
    K近邻回归（KNR）最邻近数据点数量n_neighbors5
    叶子结点个数leaf_size30
    距离计算方式p2（欧氏距离）
    岭回归（RDR）正则项系数alpha1
    是否需要计算截距fit_interceptTrue
    决策树回归（DTR）每个内部节点(非叶子节点)包含的最少的样本数min_samples_split2
    每个叶子结点包含的最少的样本数min_samples_leaf1
    树的最大深度max_depth3
    集成学习算法
    Integrated learning algorithm    		支持向量回归（SVR）多项式核函数的次数degree3
    残差收敛值tol10−4
    交叉验证次数cv10
    自适应提升回归（ABR）决策树的数量n_estimators1256
    学习率learning_rate0.2
    每个基础决策树分裂所需最小样本数min_samples_split10
    每个基础决策树叶节点所包含的最小样本数min_samples_leaf5
    极度梯度提升回归（XGR）决策树的数量n_estimators1000
    树的最大深度max_depth5
    学习率learning_rate0.1
    指定树的叶子节点上最小样本数min_child_weight3
    惩罚项系数gamma0.1
    使用的数据占训练集的比例subsample0.7
    随机森林回归（RFR）决策树的数量n_estimators1 311
    每个基础决策树分裂所需最小样本数min_samples_split2
    每个基础决策树叶节点所包含的最小样本数min_samples_leaf1
    下载: 导出CSV 
    | 显示表格

    采用SHAP法对特征变量进行筛选。SHAP 法能够提供多特征交互影响下各个特征对于预测结果的贡献值[11]。将x1～x10作为特征变量，Y作为目标变量，对8种机器学习算法预测精度进行比较并挑选出最优算法，再利用SHAP法对特征变量进行筛选组合，确定最终的调度流量决策模型（图4）。各方法及说明见表2。

    图  4  研究技术路线
    Figure  4.  Technology roadmap of this study
    下载: 全尺寸图片 幻灯片

    1）LR算法

    线性回归算法用于确定两个及多个变量之间定量关系 [18]，通用计算式为

    $$ \hat{{{y}}}={{b}}_1{{x}}_1+{{b}}_2{{x}}_2+\cdots+b_ix_i$$ (1)

    式中$\hat {{y}}$为目标变量， xi 为输入变量，bi为回归系数。

    2）KNR算法

    K近邻回归算法采用测量特征值之间距离的方法进行预测[19]，样本的回归预测输出值为

    $$\hat{{{y}}}=\frac{\left(\displaystyle\sum\nolimits _{v=1}^{S}{{w}}_v{{y}}_v\right)}{S}$$ (2)

    式中wv为样本权重，S为训练样本数， yv为第 v 个样本的输出值。

    3）RDR算法

    岭回归是一种专用于处理共线性数据的回归方法[20]，一般回归分析的(矩阵)形式如下：

    $$\hat{{{y}}}={\boldsymbol{X}}{\boldsymbol{\beta}}+{\boldsymbol{\varepsilon}}$$ (3)

    式中X 为输入变量矩阵，β 为回归系数矩阵，ε 为误差矩阵。

    4）DTR算法

    在机器学习中，决策树表示对象属性与其值之间的映射[21]。将输入空间划分为M个区域R1，R2，……，RM，选定的划分区域相应输出函数为

    $$ \hat{{{y}}}=\displaystyle\sum\nolimits_{m=1}^{M}\frac{1}{M}\displaystyle\sum\nolimits_{j\in R_m} {{y}}_m$$ (4)

    式中M为区域个数，Rm为第 m 个区域空间，j 为区域中的输入变量，ym 为区域 Rm 的目标变量输出值。

    5）SVR算法

    支持向量机用于回归问题时寻求二分法以最小化到超平面最远样本点的“距离”[24]，遵循使用核技巧转换数据的技术找到最佳输出边界。位于边界得到内的点满足：

    $$ \hat{{\boldsymbol{y}}}=w\varnothing\left({\boldsymbol{a}}\right)+{\boldsymbol{c}}$$ (5)

    式中w为权向量，a为输入变量，$\varnothing(a) $为高维特征空间，c 为偏置常数。

    6）ABR 算法

    ABR采用迭代思想，分类输出取决于这些多个分类器的组合效果[25]。构建的最终强分类器为

    $$ {{{H}}}\left({x}\right)={{\rm{sign}}}\left(\displaystyle\sum\nolimits _{{{{t}}}=1}^{{{{T}}}}{{{{\alpha}} }}_{{{{t}}}}{{{{h}}}}_{{{{t}}}}\left({g}\right)\right) $$ (6)

    式中 $ {h}_{t} $为基学习器，$ {\alpha }_{t} $为每个基学习器的权重系数，T为基学习器个数，g为输入变量。

    7）XGR算法

    XGR是一种基于CART （classification and regression tree）的Boosting类集成学习模型[26]，其目标函数为

    $$\hat{{{y}}}=\displaystyle\sum\nolimits_{d}\left({y}_{d},\displaystyle\sum\nolimits_{u=1}^{K}f_u\left(x_d\right)\right)+\displaystyle\sum\nolimits_{u}\mathrm{\varOmega}\left(f_u\right) $$ (7)

    式中d为样本个数，K为提升树个数，$ {y}_{d} $ 为第d个样本$ {x}_{d} $的预测值。$\displaystyle\sum\nolimits _{u}\varOmega \left({f}_{u}\right)$表示u颗树的复杂度。

    8）RFR算法

    随机森林回归是一种基于决策树的集成学习算法[27]，包含层次上的的随机性，进行回归预测时，从所有的特征输入值H中随机选择h个值构建每棵决策树，从这h个值中去选择优化每个分割节点时，从而降低相关性，提高预测能力。

    9）SHAP法

    SHAP是一种将传统方法与博弈论和局部解释联系起来，根据预期表示一致性和局部准确性的特征归因方法[11]。SHAP value为样本中特征的分配数值，满足等式：

    $${{Y}}_n={{y}}_{{b}}+{{f}}\left(x_n,1\right)+{{f}}\left(x_n,2\right)+\cdots+{{f}}\left(x_n,{{P}}\right) $$ (8)

    式中Yn为输出的SHAP值， yb 为所有样本目标变量的均值，f( xn, 1) 为第 n 个样本中第1个特征变量对该样本预测的贡献值，f( xn , P) 以此类推。

    1.4   数据标准化与算法评价指标

    将搜集到的180组变量数据按照4:1的比例分为训练集与测试集，调用Python 3.9进行算法预测与验证。

    1）为消除数据量纲对于研究效果的影响，模型数据采用Z-score 标准化方法，其计算式如下：

    $$ {{{{Z}}}}_{{{{B}}}}=\frac{{Z}-\overline{{{{Z}}}}}{\mathrm{{{\sigma}} }} $$ (9)

    式中${{{{Z}}}}_{{{{B}}}}$表示标准化后的数值，Z表示原始数据，$\overline{{{{Z}}}}$表示原始数据的平均数，${{{\sigma}} }$表示原始数据的标准差。

    2）为评估算法预测精度，利用灌口集泄水闸调度流量预测值与实际值之间的均方根误差（SRMSE）、平均绝对误差（SMAE）、均方误差（SMSE）和决定系数（R2）作为评价指标。其中SRMSE、SMAE和SMSE越接近0，表示模型偏差度越小；R2越接近1，表明预测值与实际值之间的吻合度越高。具体计算公式如下：

    $$ {{{S}}}_{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}=\sqrt{\frac{1}{{{{F}}}}{\displaystyle\sum\nolimits }_{{{{k}}}=1}^{{{{F}}}}{\left({{{P}}}_{{{{k}}}}-{{{R}}}_{{k}}\right)}^{2}} $$ (10)
    $$ {{{S}}}_{\mathrm{M}\mathrm{A}\mathrm{E}}\text=\frac{\text{1}}{{{{F}}}}\displaystyle\sum\nolimits _{{{{k}}}\text{=1}}^{{{{F}}}}\left(\left|{{{R}}}_{{{{k}}}}\text-{{{P}}}_{{{{k}}}}\right|\right) $$ (11)
    $$ {{{S}}}_{\mathrm{M}\mathrm{S}\mathrm{E}}=\dfrac{{\displaystyle\sum\nolimits }_{{{{k}}}}^{{{{F}}}}{({{{{P}}}}_{{{{k}}}}-{{{R}}}_{{{{k}}}})}^{2}}{{{{F}}}} $$ (12)
    $${{R}}^2=\left\{\frac{\displaystyle\sum\nolimits_{{{k}}=1}^{{{F}}}{({{P}}_{{k}}-\overline{{{P}}})({{R}}_{{k}}-\overline{{{R}}})}}{\sqrt{{{({{P}}}_{{k}}-\overline{{P})}}^2}\sqrt{({{{R}}_{{k}}-\overline{{{R}}})}^2}}\right\} $$ (13)

    式中 Rk为第k组数据的实际调度流量值；Pk为第k组数据的预测调度流量值；$\overline{{{{R}}}}$ 为Rk的平均值；$\overline{{{{P}}}}$ 为 ${{{{P}}}}_{{{{k}}}}$的平均值；${{{F}}}$为样本个数。

    2.   结果与分析

    2.1   基于不同机器算法的调度流量预测精度比较

    为了验证8种机器学习算法在整个数据集上是否适用，本研究同时对训练集和测试集进行预测，分析其SRMSE、SMAE、SMSE及R2指标并进行比较（表3）。

    表  3  基于8种算法的调度流量预测评价
    Table  3.  Prediction evaluation of dispatching flow based on 8 algorithms
    分类
    Type    		训练集 Training set测试集 Test set
    SRMSESMAESMSER2SRMSESMAESMSER2
    传统回归算法
    Traditional regression algorithm    		LR0.5180.4350.2680.7020.6090.4990.3700.727
    KNR0.4940.3830.2870.7080.5760.3830.3320.756
    RDR0.5030.4240.2600.7120.5480.4530.3010.779
    DTR0.4760.3240.2270.7240.5110.3810.2610.808
    集成学习算法
    Integrated learning algorithm    		SVR0.3380.2900.1140.8730.4630.3200.2150.842
    ABR0.3310.2920.1090.8840.4330.3380.1870.853
    XGR0.1550.0930.0240.9540.3540.2360.1260.908
    RFR0.1460.0940.0210.9760.3060.1970.0930.931
    注：SRMSE为均方根误差；SMAE为平均绝对误差；SMSE为均方误差；R2为决定系数。
    Note: SRMSE is the root mean square error; SMAE is mean absolute error. SMSE is mean square error; R2 is the coefficient of determination.
    下载: 导出CSV 
    | 显示表格

    由表3可得，传统回归算法中DTR训练集及测试集误差指标均为4种算法中最优，LR的训练集SMSE较最大的KNR仅降低了6.6%，其余指标均为4种算法中最差。因此，LR在传统回归算法中的预测精度最差。集成学习算法中SVR训练集及测试集SMAE较最大的ABR 分别降低了0.7%、5.3%，降幅不大，其余指标均为4种算法中最差。因此，SVR在4种集成学习算法中的预测精度最差。对比SVR和DTR，SVR训练集及测试集误差指标均优于DTR。综上，集成学习算法较传统回归算法预测精度更佳。集成学习算法间的预测精度也具有一定差异，RFR训练集 SRMSE、 SMAE、 SMSE、 R2分别为0.146 m3/s、0.094 m3/s、0.021 m3/s、0.976；测试集分别为0.306 m3/s、0.197 m3/s、0.093 m3/s、0.931，在集成学习算法中RFR的预测精度最高。DTR训练集 SRMSE、 SMAE、SMSE、 R2分别为0.476 m3/s、0.324 m3/s、0.227 m3/s、0.724；测试集分别为0.511 m3/s、0.381 m3/s、0.261 m3/s、0.808，相比DTR，RFR的预测精度更高。

    对比4种集成学习算法，XGR在训练集及测试集误差指标上均优于ABR，RFR的训练集SMAE 与XGR相差不大，其余指标均优于XGR，集成学习算法的预测精度排序为： RFR>XGR>ABR>SVR， 3类集成学习算法的预测精度由高到低依次为装袋算法、提升算法、堆叠算法。综上，随机森林回归（RFR）在8种算法中的预测精度最优（训练集SRMSE = 0.146 m3/s、SMAE = 0.094 m3/s、SMSE = 0.021 m3/s、R2 = 0.976，测试集SRMSE = 0.306 m3/s、SMAE = 0.197 m3/s、SMSE = 0.093 m3/s、R2 = 0.931）。

    2.2   变量筛选优化

    2.2.1   特征变量重要性分析

    机器学习算法中，特征重要性是指特征变量对目标变量的影响程度，特征的选择对机器学习算法预测精度有较大影响，数量过多和不足分别会产生过拟合、欠拟合的问题，模拟精度均无法达到最佳。为检验采用10组变量进行随机森林回归算法预测是否出现过拟合现象，本研究对10组变量进行重要性分析（表4），得到不同变量对于预测结果的影响权重，通过比较不同变量组合下随机森林回归算法预测误差指标，挑选最佳变量组合进一步优化算法。

    表  4  SHAP法特征重要性分析结果
    Table  4.  Results of features importance analysis of SHAP method
    符号SymbolsSHAP 值SHAP value
    x90.415
    x50.238
    x80.235
    x40.082
    x30.080
    x20.042
    x60.034
    x10.031
    x100.023
    x70.018
    下载: 导出CSV 
    | 显示表格

    由表4得SHAP法确定的变量组合特征重要性排序为：x9> x5>x8>x4> x3> x2> x6> x1> x10> x7， x9对预测结果的影响最大，占SHAP值总和的34.6%。过去时段降雨量（x1～x5）SHAP值总和为0.473，未来时段降雨量（x6～x8）SHAP值总和为0.287，可见过去时段降雨对泄水调度决策的影响程度比未来降雨更大。

    2.2.2   特征变量筛选

    根据表4建立10种组合分析训练集和测试集误差指标及变化趋势（表5）。由表5可以看出，不同变量组合下，RFR训练集SMSE、SMAE、SRMSE及R2均优于测试集，依次去除特征重要性最小的因素，误差指标SRMSE、SMAE、SMSE呈现出先减小后增大的趋势，R2呈现出先增大后减小的趋势。可见，当把x1～ x10作为输入变量时出现了过拟合现象，变量组合x4+ x8+ x5+ x9训练集及测试集指标均为10种组合最优，由SHAP法确定以x4+x5+ x8+ x9作为输入变量时，随机森林回归（RFR）算法的预测效果最佳（训练集SRMSE=0.126 m3/s、SMAE=0.080 m3/s、SMSE=0.016 m3/s、R2=0.982；测试集SRMSE=0.263 m3/s、SMAE = 0.164 m3/s、SMSE=0.069 m3/s、R2=0.950）。其训练集及测试集R2较采用所有特征变量预测分别提高了0.6%、2.0%；SRMSE、SMAE、SMSE分别降低了13.7%、14.9%、23.8%、14.1%、16.3%、25.8%；可见变量选择对预测精度的影响较为显著。

    表  5  基于SHAP法和RFR的10种组合训练集及测试集评价指标
    Table  5.  Evaluation metrics for 10 combined training sets and test sets based on SHAP method and RFR
    组合
    Group    		训练集Training set测试集Test set
    SRMSE/(m3·s-1)SMAE/(m3·s-1)SMSE/(m3·s-1)R2SRMSE/(m3·s-1)SMAE/(m3·s-1)SMSE/(m3·s-1)R2
    x7+x10+x1+x6+x2+x3+x4+x8+x5+x90.1460.0940.0210.9760.3060.1960.0930.931
    x10+x1+x6+x2+x3+x4+x8+x5+x90.1450.0930.0210.9770.3030.1970.0920.932
    x1+x6+x2+x3+x4+x8+x5+x90.1340.0860.0180.9800.2750.1830.0760.944
    x6+x2+x3+x4+x8+x5+x90.1300.0840.0170.9810.2700.1810.0730.946
    x2+x3+x4+x8+x5+x90.1300.0830.0170.9810.2680.1730.0720.947
    x3+x4+x8+x5+x90.1300.0820.0170.9810.2630.1700.0690.949
    x4+x8+x5+x90.1260.0800.0160.9820.2630.1640.0690.950
    x8+x5+x90.1300.0820.0170.9810.2650.1730.0700.948
    x5+x90.1950.1320.0380.9580.5110.3580.2610.808
    x90.3560.2520.1270.8590.7550.5890.5700.581
    下载: 导出CSV 
    | 显示表格

    3.   讨　论

    3.1   目标变量影响因子分析

    本研究选择的10个特征变量可归类为水位和降雨2种类型。LONG等[28]指出，水位波动对三峡大坝的日调节流量影响较大；JANE等[29]也提出，水位流量关系是分析洪水成因，进行风险评估的重要内容；纪亚星等[30]认为不同降雨重现期对理想区域的洪峰流量削减率不同；崔春光等[31]将中尺度数值模式的预报降雨信息输入新安江模型，结果表明预见期内的降水量直接影响洪水流量预报的精度，以上研究均表明水位和降雨是影响流量的重要因素。由表4可得，在特征变量重要性排列中第一位为 x9，其原因为闸上水位是影响灌口集泄水闸调度流量的直接因素，闸前水位高，其泄水流量必然趋向增大。降雨是诱发洪水的驱动因素和激发条件[32]，本研究中不同时段降雨量对泄水调度流量的影响不同，这与鲁洋等[33-34]研究一致。表4中过去时段降雨对泄水调度决策的影响程度较未来降雨更大的原因是落地雨除去损失后的净雨为产流过程，未来降雨形成的径流过程需净雨通过坡面和沟道产生，降雨先后经历该2个过程的变化，使径流的相关性弱于产流[35]。

    3.2   不同机器学习算法预测精度差异

    从表3看出，集成学习算法误差指标明显优于传统机器学习算法，这是因为传统机器学习算法中各类基学习器在不同数据源上的学习效果不同，单一基学习器对于样本的学习误差可能较大。集成学习能够训练多个基学习器模型，得到一个较好的集成模型，从而提高整个模型的泛化能力[36]，由于基学习器的种类、训练模式以及输出方法不同，集成学习算法的预测结果也不尽相同。由表3得到3类集成学习算法中装袋算法预测精度最高的原因是：特征变量和目标变量分布趋势较为相似，装袋算法对于训练模型差距不大的样本，能够通过投票或平均化最大程度还原目标值。赵敬涛等[23]采用3类集成学习算法对企业自律性进行评估，得到预测精度由高到低依次为：提升算法、装袋算法、堆叠算法，与本研究有所不同，这是因为：企业自律性评价数据集同时存在离散类和连续类特征，装袋算法的各个基学习器的输出只作一个简单的投票或平均，其学习效果有相当大的局限性[37]。而提升算法中梯度提升决策树（gradient boosting decision tree，GBDT）的每个分类器都会在上一轮训练基础上不断降低偏差，对于多特征数据集学习效果更佳。同时，赵敬涛等得到XGR预测精度优于ABR，与本研究结果一致，这是因为：ABR通过拟合残差逐渐减少残差，而XGR基于GBDT的每次计算都能减少残差，XGR较ABR可更大程度上减少误差。

    本研究对比8种机器学习算法预测评价指标，随机森林算法预测精度高于其他算法的原因可能是：1）现有的随机森林算法不需要考虑一般回归问题所面临的多元共线性问题，在部分数据缺失或数据量相对较小的情况下仍能保持一定的精度[38]；2）随机森林算法具有一定的抗噪声能力；3）时间、降雨、水位及流量间的数据维度相差较大，随机森林算法无需做特征选择，对数据集的适应能力强。HASAN等[39]以沿海地区为例，研究得到随机森林算法能够准确预估洪水敏感性，为防洪策略制定提供了可靠思路；高玮志等[40]基于KNN和随机森林算法构建流域、区域、城镇多层次调度方案综合评价模型，为防洪调度方案的优选提供科学参考。以上研究结果均证实了随机森林算法在防洪调度决策上的可行性。

    3.3   特征变量筛选对预测精度的影响

    机器学习算法模拟精度受数据集特征选择的影响[41]。STEPHEN等[42]认为合理的特征选择可以消除数据中的噪声，提高模型性能。本研究采用SHAP法对所选10组特征变量进行重要性排序，并分为10种组合进行预测对比，结果表明，采用x4+ x5+ x8+ x9作为输入变量时，随机森林回归算法预测精度最佳。同时，选用x4+ x5+ x8+ x9相比于选用全部变量也降低了数据收集成本和难度。综合2010—2020年历史数据，过去6 h降雨量、过去9 h降雨量、未来6 h降雨量、灌口集泄水闸闸上水位是影响灌口集泄水闸调度流量的主要因素。

    本研究基于机器学习构建的泄水调度决策模型，属于数据驱动型的黑箱模型，与相关的产汇流—洪水演进—泄水调度耦合性机理模型在本质上有较大区别，两者各有其优缺点，机理模型虽然能够得到诸如入渠洪水流量过程、渠道及洪水位演进等中间要素的动态变化，但其需要的水文水动力方程耦合计算过程较为复杂；机器学习虽无法得到相关水文演进过程，但其主要优点在于能够利用降雨和水位等相对易获取的监测和预报数据，快速地获取泄水闸的调度决策方案，避免了耦合机理模型所需要的多源数据搜集和预前处理。

    4.   结　论

    本研究基于安徽淠史杭灌区灌口集泄水闸调度流量及闸上水位和降雨数据，采用4种传统机器学习回归算法（线性回归（linear regression, LR）、K近邻回归（k-nearest neighbors regressor, KNR）、岭回归（ridge regression, RDR）、决策树回归（decision tree regression, DTR））和4种集成学习类算法（支持向量回归（support vector regression, SVR）、自适应提升回归（adaptive boosting regression, ABR）、极度梯度提升回归（extreme gradient boosting regression, XGR）、随机森林回归（random forest regression, RFR））进行预测对比，并通过SHAP法进行特征重要性分析，得到结论如下：

    1）集成学习算法预测评价指标优于传统回归算法，8种机器学习算法中RFR的预测精度最高（训练集均方根误差、平均绝对误差、均方误差及决定系数分别为0.146 m3/s、0.094 m3/s、0.021 m3/s、0.976，测试集分别为0.306 m3/s、0.197 m3/s、0.093 m3/s、0.931）。

    2）采用Shapley Additive exPlanations（SHAP）法确定的特征变量重要性排序表明灌口集泄水闸闸上水位对于泄水闸调度流量的预测结果影响最大，占特征重要性值总和的34.6%。

    3）以过去6 h降雨量、过去9 h降雨量、未来6 h降雨量、灌口集泄水闸闸上水位为输入变量的随机森林回归算法预测灌口集泄水闸调度流量效果最佳，模型误差指标为（训练集均方根误差、平均绝对误差、均方误差及决定系数分别为0.126 m3/s、0.080 m3/s、0.016 m3/s、0.982；测试集分别为0.263 m3/s、0.164 m3/s、0.069 m3/s、0.950）。

    本研究的不足之处在于采用SHAP法和随机森林算法构建的调度流量预测模型是针对灌区渠道特定闸门的决策模型，在考虑因素时候只选取了不同时期的降雨和水位。因此，若要将其推广至更大的下垫面区域，后续研究应将更多的变动影响因素（如流域下垫面面积、河道断面糙率、渠道断面坡度等）纳入考虑。

  • 图  1   淠史杭灌区示意图

    注：DEM为地表高程。

    Figure  1.   Schematic diagram of irrigation area of Pi Shihang

    Note: DEM is the surface elevation.

    下载: 全尺寸图片 幻灯片

    图  2   灌口集泄水单元连接关系图

    Figure  2.   Guan Kouji drainage unit connection relationship diagram

    下载: 全尺寸图片 幻灯片

    图  3   灌口集泄水闸调度流量分布曲线

    Figure  3.   Distribution curve of dispatching flow of Guan Kouji drainage gate

    下载: 全尺寸图片 幻灯片

    图  4   研究技术路线

    Figure  4.   Technology roadmap of this study

    下载: 全尺寸图片 幻灯片

    表  1   变量及说明

    Table  1   Variables and descriptions

    符号
    Symbols    		说明
    Description    		单位
    Units    		数据系列长度
    Data series length
    x1过去1 h降雨量mm2010—2020年
    x2过去2 h降雨量mm
    x3过去3 h降雨量mm
    x4过去6 h降雨量mm
    x5过去9 h降雨量mm
    x6未来1 h降雨量mm
    x7未来3 h降雨量mm
    x8未来6 h降雨量mm
    x9灌口集泄水闸闸上水位m
    x10过去0.5 h闸上水位差m
    Y灌口集泄水闸调度流量m3·s−1
    下载: 导出CSV

    表  2   算法参数及说明

    Table  2   Algorithm parameters and description

    分类 Type算法 Algorithm参数及解释 Parameter and its explanation取值 Value
    传统回归算法
    Traditionl regression algorithm    		线性回归（LR）是否需要计算截距fit_interceptTrue
    是否复制训练数据copy_XTrue
    K近邻回归（KNR）最邻近数据点数量n_neighbors5
    叶子结点个数leaf_size30
    距离计算方式p2（欧氏距离）
    岭回归（RDR）正则项系数alpha1
    是否需要计算截距fit_interceptTrue
    决策树回归（DTR）每个内部节点(非叶子节点)包含的最少的样本数min_samples_split2
    每个叶子结点包含的最少的样本数min_samples_leaf1
    树的最大深度max_depth3
    集成学习算法
    Integrated learning algorithm    		支持向量回归（SVR）多项式核函数的次数degree3
    残差收敛值tol10−4
    交叉验证次数cv10
    自适应提升回归（ABR）决策树的数量n_estimators1256
    学习率learning_rate0.2
    每个基础决策树分裂所需最小样本数min_samples_split10
    每个基础决策树叶节点所包含的最小样本数min_samples_leaf5
    极度梯度提升回归（XGR）决策树的数量n_estimators1000
    树的最大深度max_depth5
    学习率learning_rate0.1
    指定树的叶子节点上最小样本数min_child_weight3
    惩罚项系数gamma0.1
    使用的数据占训练集的比例subsample0.7
    随机森林回归（RFR）决策树的数量n_estimators1 311
    每个基础决策树分裂所需最小样本数min_samples_split2
    每个基础决策树叶节点所包含的最小样本数min_samples_leaf1
    下载: 导出CSV

    表  3   基于8种算法的调度流量预测评价

    Table  3   Prediction evaluation of dispatching flow based on 8 algorithms

    分类
    Type    		训练集 Training set测试集 Test set
    SRMSESMAESMSER2SRMSESMAESMSER2
    传统回归算法
    Traditional regression algorithm    		LR0.5180.4350.2680.7020.6090.4990.3700.727
    KNR0.4940.3830.2870.7080.5760.3830.3320.756
    RDR0.5030.4240.2600.7120.5480.4530.3010.779
    DTR0.4760.3240.2270.7240.5110.3810.2610.808
    集成学习算法
    Integrated learning algorithm    		SVR0.3380.2900.1140.8730.4630.3200.2150.842
    ABR0.3310.2920.1090.8840.4330.3380.1870.853
    XGR0.1550.0930.0240.9540.3540.2360.1260.908
    RFR0.1460.0940.0210.9760.3060.1970.0930.931
    注：SRMSE为均方根误差；SMAE为平均绝对误差；SMSE为均方误差；R2为决定系数。
    Note: SRMSE is the root mean square error; SMAE is mean absolute error. SMSE is mean square error; R2 is the coefficient of determination.
    下载: 导出CSV

    表  4   SHAP法特征重要性分析结果

    Table  4   Results of features importance analysis of SHAP method

    符号SymbolsSHAP 值SHAP value
    x90.415
    x50.238
    x80.235
    x40.082
    x30.080
    x20.042
    x60.034
    x10.031
    x100.023
    x70.018
    下载: 导出CSV

    表  5   基于SHAP法和RFR的10种组合训练集及测试集评价指标

    Table  5   Evaluation metrics for 10 combined training sets and test sets based on SHAP method and RFR

    组合
    Group    		训练集Training set测试集Test set
    SRMSE/(m3·s-1)SMAE/(m3·s-1)SMSE/(m3·s-1)R2SRMSE/(m3·s-1)SMAE/(m3·s-1)SMSE/(m3·s-1)R2
    x7+x10+x1+x6+x2+x3+x4+x8+x5+x90.1460.0940.0210.9760.3060.1960.0930.931
    x10+x1+x6+x2+x3+x4+x8+x5+x90.1450.0930.0210.9770.3030.1970.0920.932
    x1+x6+x2+x3+x4+x8+x5+x90.1340.0860.0180.9800.2750.1830.0760.944
    x6+x2+x3+x4+x8+x5+x90.1300.0840.0170.9810.2700.1810.0730.946
    x2+x3+x4+x8+x5+x90.1300.0830.0170.9810.2680.1730.0720.947
    x3+x4+x8+x5+x90.1300.0820.0170.9810.2630.1700.0690.949
    x4+x8+x5+x90.1260.0800.0160.9820.2630.1640.0690.950
    x8+x5+x90.1300.0820.0170.9810.2650.1730.0700.948
    x5+x90.1950.1320.0380.9580.5110.3580.2610.808
    x90.3560.2520.1270.8590.7550.5890.5700.581
    下载: 导出CSV
    • 参考文献(42)
  • [1] 周建中,顿晓晗,张勇传. 基于库容风险频率曲线的水库群联合防洪调度研究[J]. 水利学报,2019,50(11):1318-1325. ZHOU Jianzhong, DUN Xiaohan, ZHANG Yongchan. Study on joint flood control dispatching of reservoir groups based on reservoir capacity risk frequency curve [J]. Journal of Hydraulic Engineering, 2019, 50(11): 1318-1325. (in Chinese with English abstract

    ZHOU Jianzhong, DUN Xiaohan, ZHANG Yongchan. Research on joint flood control and scheduling of reservoir group based on reservoir risk frequency curve[J]. Journal of Water Resources, 2019, 50(11): 1318-1325. (in Chinese with English abstract)
    [2] 王文川,田维璨,徐雷,等. Mε-OIDE求解约束优化问题算法及其在水库群防洪调度中的应用[J]. 水利学报,2023,54(2):148-158. WANG Wenchuan, TIAN Weican, XU Lei, et al. Mε-OIDE algorithm for solving constrained optimization problems and its application in flood control operation of reservoir group[J]. Journal of Hydraulic Engineering, 2023, 54(2): 148-158. (in Chinese with English abstract

    WANG Wenchuan, TIAN Weican, XU Lei, et al. Mε-OIDE algorithm for solving constrained optimization problems and its application in reservoir group flood control scheduling [J]. Journal of Water Resources, 2023, 54(02): 148-158. (in Chinese with English abstract)
    [3] 李其梁,苑希民,杨敏,等. 淮沂水系洪泽湖-骆马湖水资源联合优化调度研究[J]. 南水北调与水利科技,2013,11(2):10-13,23. LI Qiliang, YUAN Ximin, YANG Min, et al. Research on Optimal Regulation of Water Resources in the Hongze and Luoma Lakes of Huaiyi Water System[J]. South-to-North Water Transfers and Water Science & Technology, 2013, 11(2): 10-13,23. (in Chinese with English abstract

    LI Qiliang, YUAN Ximin, YANG Min, et al. Study on the joint optimal scheduling of water resources of Hongze Lake and Luoma Lake in Huaiyi Water System[J]. South-North Water Diversion and Water Conservancy Science and Technology, 2013, 11(02): 10-13, 23. (in Chinese with English abstract)
    [4] 林瑜,吕海深,朱永华,等. 融冰洪水演进的马斯京根模型[J]. 水资源与水工程学报,2021,32(4):86-92. LIN Yu, LV Haishen, ZHU Yonghua, et al. Simulation of ice-thawing flood by Muskingum routing model[J]. Journal of Water Resources & Water Engineering, 2021, 32(4): 86-92. (in Chinese with English abstract

    LIN Yu, LV Haishen, ZHU Yonghua, et al. A Maskingen model for the evolution of melting ice floods[J]. Journal of Water Resources and Water Engineering, 2021, 32(04): 86-92. (in Chinese with English abstract)
    [5]

    ZHAO T T G, ZHAO J S, LEI X H, et al. Improved dynamic programming for reservoir flood control operation[J]. Water Resources Management, 2017, 31(7): 2047-2063. DOI: 10.1007/s11269-017-1599-4
    [6]

    LIU X Y, CHEN L, ZHU Y H, et al. Multi-objective reservoir operation during flood season considering spillway optimization[J]. Journal of Hydrology, 2017, 552: 554-563. DOI: 10.1016/j.jhydrol.2017.06.044
    [7]

    AFAN H A, ALLAWI M F, EI S A, et al. Input attributes optimization using the feasibility of genetic nature inspired algorithm: Application of river flow forecasting.[J]. Scientific Reports, 2020, 10(1): 4684. DOI: 10.1038/s41598-020-61355-x
    [8]

    YALEZO N, MUSEE N. Meta-analysis of engineered nanoparticles dynamic aggregation in freshwater-like systems using machine learning techniques[J]. Journal of Environmental Management, 2023, 337: 1-11.
    [9] 高玮志,高华勇,王兆礼,等. 基于机器学习的太湖流域多层次防洪调度方案综合评价[J]. 水资源保护,2023,39(3):118-125. GAO Weizhi, GAO Huayong, WANG Zhaoli, et al. Comprehensive evaluation of multi-level flood control operation schemes in the Taihu Lake Basin based on machine learning[J]. Water Resources Protection, 2023, 39(3): 118-125. (in Chinese with English abstract

    GAO Weizhi, GAO Huayong, WANG Zhaoli, et al. Comprehensive evaluation of multi-level flood control scheduling scheme in Taihu Lake basin based on machine learning[J]. Water Resources Conservation, 2023, 39(3): 118-125.
    [10] 张帆,张永勇,陈俊旭,等. 多种机器学习模型对不同洪水类型特征指标模拟效果评估[J]. 地理科学进展,2022,41(7):1239-1250. ZHANG Fan, ZHANG Yongyong, CHEN Junxu, et al. Performance of multiple machine learning model simulation of process characteristic indicators of different flood types[J]. Progress in Geography, 2022, 41(7): 1239-1250. (in Chinese with English abstract

    ZHANG Fan, ZHANG Yongyong, CHEN Junxu, et al. Evaluation of multiple machine learning models for simulating the effectiveness of different flood type feature indicators[J]. Advances in Geosciences, 2022, 41(7): 1239-1250.
    [11] 周亚男,陈绘,刘洪斌. 基于多源数据和Stacking-SHAP方法的山地丘陵区土地覆被分类[J]. 农业工程学报,2022,38(23):213-222. ZHOU Yanan, CHEN Hui, LIU Hongbin. Land cover classification in hilly and mountainous areas using multi-source data and Stacking-SHAP technique[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(23): 213-222. (in Chinese with English abstract

    ZHOU Yanan, CHEN Hui, LIU Hongbin. Land cover classification in mountainous hilly areas based on multi-source data and Stacking-SHAP method[J]. Journal of Agricultural Engineering, 2022, 38(23): 213-222. (in Chinese with English abstract)
    [12]

    FAN Z Y, JIANG J M, CHEN X, et al. Construction and validation of prognostic models in critically Ill patients with sepsis-associated acute kidney injury: interpretable machine learning approach[J]. Journal of translational medicine, 2023, 21(1): 406. DOI: 10.1186/s12967-023-04205-4
    [13] 李心雨,闫浩文,王卓,等. 街景图像与机器学习相结合的道路环境安全感知评价与影响因素分析[J]. 地球信息科学学报,2023,25(4):852-865. LI Xinyu, YAN Haowen, WANG Zhuo, et al. Evaluation of road environment safety perception and analysis of influencing factors combining street view imagery and machine learning[J]. Journal of Geo- information Science, 2023, 25(4): 852-865. (in Chinese with English abstract

    LI Xinyu, YAN Haowen, WANG Zhuo, et al. A combination of streetscape images and machine learning for road environment safety perception evaluation and influence factor analysis[J]. Journal of Geoinformation Science, 2023, 25(4): 852-865. (in Chinese with English abstract)
    [14] 刘贺,郭黎,李豪,等. 面实体匹配的集成学习CatBoost方法[J]. 地球信息科学学报,2022,24(11):2198-2211. LIU He, GUO Li, LI Hao, et al. Matching areal entities with catboost ensemble method[J]. Journal of Geo-information Science, 2022, 24(11): 2198-2211. (in Chinese with English abstract

    LIU He, GUO Li, LI Hao, et al. Integrated learning CatBoost method for surface entity matching[J]. Journal of Geoinformation Science, 2022, 24(11): 2198-2211. (in Chinese with English abstract)
    [15] 王顺利. 丰乐水库灌区南干渠防洪问题与对策[J]. 江淮水利科技,2012,37(1):22-24. WANG Shunli. Flood control problems and countermeasures in the south trunk canal of Fengle reservoir irrigation area[J]. Jianghuai Water Resources Science and Technology, 2012, 37(1): 22-24. (in Chinese with English abstract

    WANG Shunli. Flood control problems and countermeasures in the south trunk canal of Fengle reservoir irrigation area [J]. Jianghuai Water Conservancy Science and Technology, 2012, 37(1): 22-24. (in Chinese with English abstract)
    [16] 范营营. MIKE11在泄洪闸闸宽比选中的应用-以江西省某灌区为例[J]. 海河水利,2022(6):102-105,116. FAN Yingying. Application of MIKE11 hydrodynamic model in the width comparisonof Spillway Gate—Taking an irrigation district in Jiangxi Province as the Case[J]. Haihe Water Resourcess, 2022(6): 102-105,116. (in Chinese with English abstract

    FAN Yingying. Application of MIKE11 in floodgate gate width ratio checking--an example of an irrigation district in Jiangxi Province [J]. Haihe Water Resources, 2022(6): 102-105, 116. (in Chinese with English abstract)
    [17]

    GE J K, ZHAO L F, YU Z H, et al. Prediction of greenhouse tomato crop evapotranspiration using XGBoost machine learning model.[J]. Plants (Basel, Switzerland), 2022, 11(15): 1923.
    [18] 宗成骥,王建玉,宋卫堂,等. 基于天气预报的日光温室夜间逐时气温预测模型构建[J]. 农业工程学报,2022,38(S1):218-225. ZONG Chengji, WANG Jianyu, SONG Weitang, et al. Construction and validation of hourly air temperature prediction model in solar greenhouse at night[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(S1): 218-225. (in Chinese with English abstract

    ZONG Chengji, WANG Jianyu, SONG Weitang, et al. Construction of a model for predicting night-time hour-by-hour temperature of heliostat based on weather forecasting[J]. Journal of Agricultural Engineering, 2022, 38(S1): 218-225. (in Chinese with English abstract)
    [19] 李芬芳,汝春瑞,党小超,等. 基于CSI和加权混合回归的室内定位方法[J]. 传感技术学报,2022,35(5):667-675. LI Fenfang, RU Chunrui, DANG Xiaochao, et al. Indoor localization method based on csi and weighted mixed regression[J]. Chinese Journal of Sensors and Actuators, 2022, 35(5): 667-675. (in Chinese with English abstract

    LI Fenfang, RU Chunrui, DANG Xiaochao, et al. An indoor localization method based on CSI and weighted mixed regression[J]. Journal of Sensing Technology, 2022, 35(5): 667-675. (in Chinese with English abstract)
    [20] 彭涛,赵丽,张爱军,等. 土壤全氮的无人机高光谱响应特征及估测模型构建[J]. 农业工程学报,2023,39(4):92-101. PENG Tao, ZHAO Li, ZHANG Aijun, et al. UAV hyperspectral response characteristics and estimation model construction of soil total nitrogen[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(4): 92-101. (in Chinese with English abstract

    PENG Tao, ZHAO Li, ZHANG Aijun, et al. UAV hyperspectral response characteristics of soil total nitrogen and estimation model construction[J]. Journal of Agricultural Engineering, 2023, 39(4): 92-101. (in Chinese with English abstract)
    [21] 吕超,孙佳新,刘爽. 利用机器学习算法的海洋渔船捕捞能力影响因素权重分析[J]. 农业工程学报,2021,37(13):135-141. LYU Chao, SUN Jiaxin, LIU Shuang. Weight analysis of influencing factors of fishing capacity of marine fishing vessels using machine learning algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(13): 135-141. (in Chinese with English abstract

    LV Chao, SUN Jiaxin, LIU Shuang. Weight analysis of factors affecting fishing capacity of Marine fishing vessels using machine learning algorithm [J]. Journal of Agricultural Engineering, 2021, 37(13): 135-141.
    [22] 吴彤,李勇,葛莹,等. 利用Stacking集成学习估算柑橘叶片氮含量[J]. 农业工程学报,2021,37(13):163-171. WU Tong, LI Yong, GE Ying, et al. Estimation of nitrogen contents in citrus leaves using Stacking ensemble learning[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(13): 163-171. (in Chinese with English abstract

    WU Tong, LI Yong, GE Ying, et al. Estimation of nitrogen content in citrus leaves using Stacking integrated learning[J]. Journal of Agricultural Engineering, 2021, 37(13): 163-171. (in Chinese with English abstract)
    [23] 赵敬涛, 赵泽方, 岳兆娟, 等. TenrepNN: 集成学习的新范式在企业自律性评价中的实践[J/OL]. 计算机应用: 1-8[2023-03-23]. http: //kns.cnki.net/kcms/detail/51.1307.TP.20230316.1329.004.html

    ZHAO Jingtao, ZHAO Zefang, YUE Zhaojuan, et al. TenrepNN: Practice of new ensemble learning paradigm in enterprise self-discipline evaluation [J/OL].Journal of Computer Applications: 1-8[2023-03-23]. http://kns.cnki.net/kcms/detail/51.1307.TP.20230316.1329.004.html (in Chinese with English abstract)
    [24] 杨玮,兰红,李民赞,等. 基于图像处理和SVR的土壤容重与土壤孔隙度预测[J]. 农业工程学报,2021,37(12):144-151. YANG Wei, LAN Hong, LI Minzan, et al. Predicting bulk density and porosity of soil using image processing and support vector regression[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(12): 144-151. (in Chinese with English abstract

    YANG Wei, LAN Hong, LI Minzan, et al. Prediction of soil capacitance and soil porosity based on image processing and SVR[J]. Journal of Agricultural Engineering, 2021, 37(12): 144-151. (in Chinese with English abstract)
    [25] 张通,金秀,饶元,等. 基于无人机多光谱的大豆旗叶光合作用量子产量反演方法[J]. 农业工程学报,2022,38(13):150-157. ZHANG Tong, JIN Xiu, RAO Yuan, et al. Inversing photosynthesis quantum yield of the soybean flag leaf using a UAV-carrying multispectral camera[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(13): 150-157. (in Chinese with English abstract

    ZHANG Tong, JIN Xiu, RAO Yuan, et al. Quantum yield inversion method for photosynthesis of soybean flag leaf based on UAV multispectral[J]. Journal of Agricultural Engineering, 2022, 38(13): 150-157. (in Chinese with English abstract)
    [26] 付波霖,孙军,李雨阳,等. 基于多光谱影像和机器学习算法的红树林树种LAI估算[J]. 农业工程学报,2022,38(7):218-228. FU Bolin, SUN Jun, LI Yuyang, et al. Mangrove LAI estimation based on remote sensing images and machine learning algorithms[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(7): 218-228. (in Chinese with English abstract

    FU Bolin, SUN Jun, LI Yuyang, et al. LAI estimation of mangrove tree species based on multispectral images and machine learning algorithms[J]. Journal of Agricultural Engineering, 2022, 38(7): 218-228. (in Chinese with English abstract)
    [27] 赵越,徐大伟,范凯凯,等. Landsat 8和机器学习估算蒙古高原草地地上生物量[J]. 农业工程学报,2022,38(24):138-144. ZHAO Yue, XU Dawei, FAN Kaikai, et al. Estimating above-ground biomass in grassland using Landsat 8 and machine learning in Mongolian plateau[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(24): 138-144. (in Chinese with English abstract

    ZHAO Yue, XU Dawei, FAN Kaikai, et al. Landsat 8 and machine learning for estimating above-ground biomass of grasslands on the Mongolian plateau [J]. Journal of Agricultural Engineering, 2022, 38(24): 138-144. (in Chinese with English abstract)
    [28]

    LONG L H, LONG L H, Ji D B, et al. Tributary oscillations generated by diurnal discharge regulation in Three Gorges Reservoir[J]. Environmental Research Letters, 2020, 15(8): 1-8.
    [29]

    JANE R A, MALAGON S V, RASHID M, et al. A hybrid framework for rapidly locating transition zones: A comparison of event‐ and response‐based return water levels in the Suwannee River FL[J]. Water Resources Research, 2022, 58(11): 1-41.
    [30] 纪亚星,同玉,侯精明,等. 西咸新区海绵城市建设对沣河洪水特性影响模拟研究[J]. 水资源与水工程学报,2021,32(2):50-57. JI Yaxing, TONG Yu, HOU Jingming, et al. Effects of sponge city construction on flood characteristics of Fenghe River in Xixian New Area[J]. Journal of Water Resources and Water Engineering, 2021, 32(2): 50-57. (in Chinese with English abstract

    JI Yaxing, TONG Yu, HOU Jingming, et al. Simulation study on the impact of sponge city construction in Xi'an New Area on flood characteristics of Fenghe River[J]. Journal of Water Resources and Water Engineering, 2021, 32(2): 50-57. (in Chinese with English abstract)
    [31] 崔春光,彭涛,沈铁元,等. 定量降水预报与水文模型耦合的中小流域汛期洪水预报试验[J]. 气象,2010,36(12):56-61. CUI Chunguang, PENG Tao, SHEN Tieyuan, et al. The Flood Forecast Test on QPF Coupling with Hydrological Model in Season in Meaium and Small Catchment[J]. Meteorological Monthly, 2010, 36(12): 56-61. (in Chinese with English abstract

    CUI Chunguang, PENG Tao, SHEN Tieyuan, et al. Experimental flood forecasting in small and medium-sized watersheds with coupled quantitative precipitation forecasting and hydrological models[J]. Meteorology, 2010, 36(12): 56-61. (in Chinese with English abstract)
    [32]

    BANFI F, DE M C. Compound flood hazard at Lake Como, Italy, is driven by temporal clustering of rainfall events[J]. Communications Earth & Environment, 2022, 3(1): 1-10.
    [33] 鲁洋,涂俊,高震国,等. 降雨时间分辨率对SWAT水文模拟的影响[J]. 中国环境科学,2020,40(12):5383-5390. LU Yang, TU Jun, GAO Zhenguo, et al. Impact of temporal rainfall resolution on SWAT hydrological simulation[J]. China Environmental Science, 2020, 40(12): 5383-5390. (in Chinese with English abstract

    LU Yang, TU Jun, GAO Zhenguo, et al. Impact of rainfall temporal resolution on SWAT hydrological simulation[J]. China Environmental Science, 2020, 40(12): 5383-5390. (in Chinese with English abstract)
    [34] 梁忠民,蒋晓蕾,曹炎煦,等. 考虑降雨不确定性的洪水概率预报方法[J]. 河海大学学报(自然科学版),2016,44(1):8-12. LIANG Zhongmin, JIANG Xiaolei, CAO Yanxu, et al. Probabilistic flood forecasting considering rainfall uncertainty[J]. Journal of Hohai University(Natural Sciences), 2016, 44(1): 8-12. (in Chinese with English abstract

    LIANG Zhongmin, JIANG Xiaolei, CAO Yanxu, et al. A probabilistic flood forecasting method considering rainfall uncertainty[J]. Journal of Riverhead University (Natural Science Edition), 2016, 44(1): 8-12. (in Chinese with English abstract)
    [35] 马亚丽,牛最荣,王兴繁,等. 缺资料地区产流径流时空特性分析及其关系研究—以洮河流域为例[J]. 水资源与水工程学报,2023,34(1):58-65. MA Yali, NIU Zuirong, WANG Xingfan, et al. Spatio-temporal characteristics of water yield and runoff and their relationship in regions with scarce data: A case study of Taohe River Basin[J]. Journal of Water Resources and Water Engineering, 2023, 34(1): 58-65. (in Chinese with English abstract

    MA Yali, NIU Zuirong, WANG Xingfan, et al. Analysis of spatial and temporal characteristics of runoff production and its relationship in data deficient areas--Take Taohe River Basin as an example[J]. Journal of Water Resources and Water Engineering, 2023, 34(1): 58-65. (in Chinese with English abstract)
    [36] 姜正申,刘宏志,付彬,等. 集成学习的泛化误差和AUC分解理论及其在权重优化中的应用[J]. 计算机学报,2019,42(1):1-15. JIANG Zhengshen, LIU Hongzhi, FU Bin, et al. Decomposition theories of generalization error and auc in ensemble learning with application in weight optimization[J]. Chinese Journal of Computers, 2019, 42(1): 1-15. (in Chinese with English abstract

    JIANG Zhengshen, LIU Hongzhi, FU Bin, et al. Integrated learning of generalization error and AUC decomposition theory and its application in weight optimization[J]. Journal of Computer Science, 2019, 42(1): 1-15. (in Chinese with English abstract)
    [37]

    AGARWAL S, CHOWDARY R C. A-stacking and a-bagging: Adaptive versions of ensemble learning algorithms for spoof fingerprint detection[J]. Expert Systems With Applications, 2020, 146(C): 113160.
    [38]

    LIANG Z M, Tang T T, LI B Q, et al. Long-term streamflow forecasting using SWAT through the integration of the random forests precipitation generator: Case study of Danjiangkou Reservoir[J]. Hydrology Research, 2018, 49(5): 1513-1527. DOI: 10.2166/nh.2017.085
    [39]

    HASAN M, AHMED A, NAFEE K M, et al. Use of machine learning algorithms to assess flood susceptibility in the coastal area of Bangladesh[J]. Ocean and Coastal Management, 2023, 236: 106503. DOI: 10.1016/j.ocecoaman.2023.106503
    [40] 高玮志, 高华勇, 王兆礼, 等. 基于机器学习的多层次防洪调度方案综合评价研究[J/OL]. 水资源保护: 1-13[2023-04-02]. http: //kns.cnki.net/kcms/detail/32.1356.TV.20220706.1801.008.html

    GAO Weizhi, GAO Huayong, WANG Zhaoli, et al. Comprehensive evaluation of multiscale flood control dispatching schemes based on machine learning[J/OL]. Water Resources Protection: 1-13[2023-04-02]. http://kns.cnki.net/kcms/detail/32.1356.TV.20220706.1801.008.html (in Chinese with English abstract)
    [41]

    GIRISH C K, FERAT S. A survey on feature selection methods[J]. Computers and Electrical Engineering, 2014, 40(1): 16-28. DOI: 10.1016/j.compeleceng.2013.11.024
    [42]

    STEPHEN A, PETER A, BELING. A survey of feature selection methods for Gaussian mixture models and hidden Markov models[J]. Artificial Intelligence Review, 2019, 52(3): 1739-1779. DOI: 10.1007/s10462-017-9581-3
    • 相关文章
    • 施引文献(11)

  • 期刊类型引用(7)

    1. 朱志畅，葛焱，臧晶荣，李庆，金时超，徐焕良，翟肇裕. 基于无人机图像和SHAP特征筛选的小麦田间产量预测方法研究. 麦类作物学报. 2025(02): 264-274 . 百度学术
    2. 刘亚栋，刘贤，胡贺松，陈航，乔升访. 基于可解释机器学习模型的基坑围护墙变形影响因素分析. 中国安全科学学报. 2025(04): 110-119 . 百度学术
    3. 邢卓冉，张凯，刘旭东，马明，刘冰洋，丁松爽，时雅琪，安继鹏，高浩杰，时向东. 基于随机森林特征优选的雪茄烟叶晾制过程含水率预测. 农业工程学报. 2024(07): 343-354 . 本站查看
    4. 杨楠，石红燕. 基于数值模拟的放水闸稳定性分析及防渗研究. 水利科技与经济. 2024(07): 42-47 . 百度学术
    5. 韩坤，王惟璐，黄雪峰，李鹏海，李春生，郑俊林. 基于NGO-CNN-SVM的高标准农田灌溉工程施工成本预测. 农业工程学报. 2024(14): 62-72 . 本站查看
    6. 焦鹏华，牛健植，苗禹博，李君宜，王迪. 2001—2020年全球植被对极端气候的响应. 应用生态学报. 2024(11): 2992-3004 . 百度学术
    7. 陈鹏，庞力文，黄凯. 基于机器学习与SHAP的油气储运事故风险分析. 现代职业安全. 2023(09): 82-86 . 百度学术

    其他类型引用(4)

    • 资源附件(0)
图(4)  /  表(5)
计量
  • 文章访问数:  0
  • HTML全文浏览量:  2
  • PDF下载量:  0
  • 被引次数: 11
出版历程
  • 收稿日期:  2023-04-10
  • 修回日期:  2023-05-08
  • 网络出版日期:  2023-07-24
  • 刊出日期:  2023-07-14

目录

摘要
HTML全文

  • 0.   引　言

  • 1.   材料与方法

  • 1.1   研究区概况

  • 1.2   影响因素分析和数据来源

  • 1.3   研究方法

  • 1.4   数据标准化与算法评价指标

  • 2.   结果与分析

  • 2.1   基于不同机器算法的调度流量预测精度比较

  • 2.2   变量筛选优化

  • 2.2.1   特征变量重要性分析
  • 2.2.2   特征变量筛选

  • 3.   讨　论

  • 3.1   目标变量影响因子分析

  • 3.2   不同机器学习算法预测精度差异

  • 3.3   特征变量筛选对预测精度的影响

  • 4.   结　论

参考文献(42)
相关文章
施引文献(11)
资源附件(0)

/

返回文章
返回

友情链接

农机院
卓众二维码
中国农业工程学会二维码
中国农业机械学会二维码

本系统由 北京仁和汇智信息技术有限公司 开发  百度统计